Cálculo básico de componentes electrónicos

En el apasionante mundo de la electrónica, cada dispositivo y circuito es como un intrincado rompecabezas de componentes interconectados. Para cualquier entusiasta de la tecnología, comprender cómo funcionan y cómo interactúan estos componentes es fundamental. Desde resistencias hasta condensadores y más allá, el cálculo básico de componentes electrónicos es el punto de partida esencial para desentrañar los secretos detrás de la creación y operación de dispositivos electrónicos. En este blog, vamos a adentrarnos en el fascinante reino de los componentes electrónicos, explorando los conceptos clave que nos permitirán comprender su comportamiento y aplicaciones en el mundo real.

Suma de Resistencias en Serie:

Cuando las resistencias están en serie, se suman simplemente para obtener la resistencia total. Es como poner una detrás de otra en un camino.

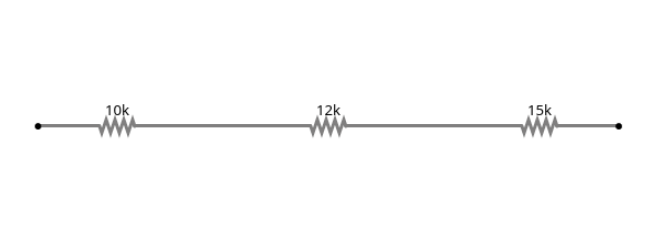
Fórmula para Resistencias en Serie:

Por ejemplo, si R₁= 10 kΩ, R₂= 12 kΩ y R₃= 15 kΩ:

R_total = R₁ + R₂ + R₃ + ...

R_total= 10 kΩ + 12 kΩ + 15 kΩ = 37 kΩ

Suma de Resistencias en Paralelo:

Cuando las resistencias están en paralelo, el cálculo es un poco más complicado. La resistencia total es menor que la resistencia más pequeña en el conjunto.

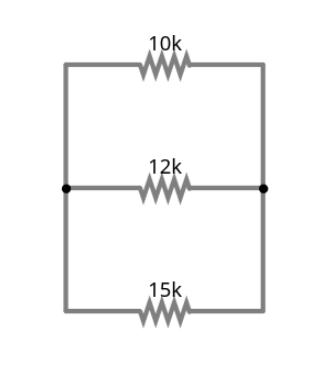
Fórmula para Resistencias en Paralelo:

¹/_Rtotal = ¹/_R1 + ¹/_R2 + ¹/_R3 + ...

Utilizando los valores R₁= 10 kΩ, R₂= 12 kΩ y R₃= 15 kΩ:

¹/_Rtotal = ¹/_{10 kΩ} + ¹/_{12 kΩ} + ¹/_{15 kΩ}

1. Multiplica cada fracción por el producto de los denominadores restantes:

\( \frac{1}{R_{\text{total}}} = \frac{12 \cdot 15}{10 \cdot 12 \cdot 15} + \frac{10 \cdot 15}{10 \cdot 12 \cdot 15} + \frac{10 \cdot 12}{10 \cdot 12 \cdot 15} \)

2. Suma los numeradores de las fracciones resultantes:

\( \frac{1}{R_{\text{total}}} = \frac{180}{10 \cdot 12 \cdot 15} + \frac{150}{10 \cdot 12 \cdot 15} + \frac{120}{10 \cdot 12 \cdot 15} \)

3. Continúa sumando los numeradores:

\( \frac{1}{R_{\text{total}}} = \frac{180 + 150 + 120}{10 \cdot 12 \cdot 15} \)

4. Suma los numeradores finales:

\( \frac{1}{R_{\text{total}}} = \frac{450}{10 \cdot 12 \cdot 15} \)

5. Simplifica el denominador:

\( \frac{1}{R_{\text{total}}} = \frac{3}{12} \, \text{S} \)

6. Toma el recíproco para obtener la resistencia total:

\( R_{\text{total}} = \frac{1}{\frac{3}{12}} \, \text{k}\Omega \)

\( R_{\text{total}} = \frac{12}{3} \, \text{k}\Omega \)

\( R_{\text{total}} \)= \(4 \, \text{k}\Omega\)

Suma de Capacitores en Serie:

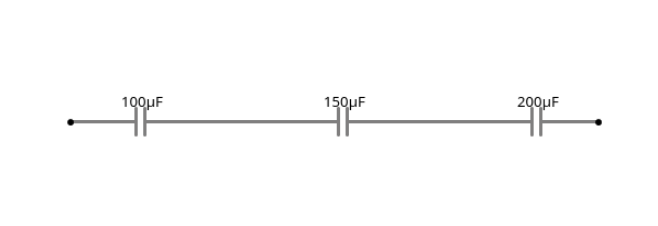
Fórmula para Capacitores en Serie

Dado: C₁ = 100 μF, C₂ = 150 μF, C₃ = 200 μF

1. La fórmula correcta para capacitores en serie involucra el uso del inverso de las capacitancias:

\( \frac{1}{C_{\text{total}}} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} \)

2. Sustituye los valores dados:

\( \frac{1}{C_{\text{total}}} = \frac{1}{100 \, \mu\text{F}} + \frac{1}{150 \, \mu\text{F}} + \frac{1}{200 \, \mu\text{F}} \)

3. Calcula la suma de los inversos:

\( \frac{1}{C_{\text{total}}} = \frac{100 \cdot 150}{100 \cdot 150 \cdot 200} + \frac{100 \cdot 200}{100 \cdot 150 \cdot 200} + \frac{150 \cdot 200}{100 \cdot 150 \cdot 200} \, \text{F}^{-1} \)

\( \frac{1}{C_{\text{total}}} = \frac{15000}{100 \cdot 150 \cdot 200} + \frac{20000}{100 \cdot 150 \cdot 200} + \frac{30000}{100 \cdot 150 \cdot 200} \, \text{F}^{-1} \)

\( \frac{1}{C_{\text{total}}} = \frac{15000 + 20000 + 30000}{100 \cdot 150 \cdot 200} \, \text{F}^{-1} \)

\( \frac{1}{C_{\text{total}}} = \frac{65000}{100 \cdot 150 \cdot 200} \, \text{F}^{-1} \)

\( \frac{1}{C_{\text{total}}} = \frac{13}{600} \, \text{F}^{-1} \)

4. Toma el recíproco para encontrar \(C_{\text{total}}\):

\( C_{\text{total}} = \frac{1}{\frac{13}{600}} \, \mu\text{F} \)

\( C_{\text{total}} = \frac{600}{13} \, \mu\text{F} \)

\( C_{\text{total}}\) = \( \frac{600}{13} \, \mu\text{F} \approx 46.15 \, \mu\text{F} \)

Suma de Capacitores en Paralelo:

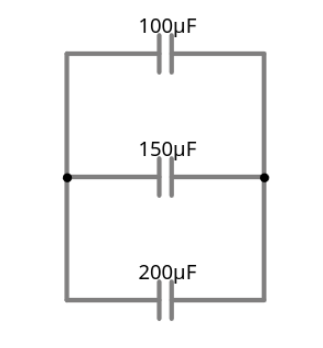
Fórmula para Capacitores en Paralelo

Dado: C₁ = 100 μF, C₂ = 150 μF, C₃ = 200 μF

1. La fórmula para capacitores en paralelo es la suma simple de las capacitancias:

\( C_{\text{total}} = C_1 + C_2 + C_3 \)

2. Sustituye los valores dados:

\( C_{\text{total}} = 100 \, \mu\text{F} + 150 \, \mu\text{F} + 200 \, \mu\text{F} \)

3. Calcula la suma:

\( C_{\text{total}} = 450 \, \mu\text{F} \)

Suma de Inductancias en Serie:

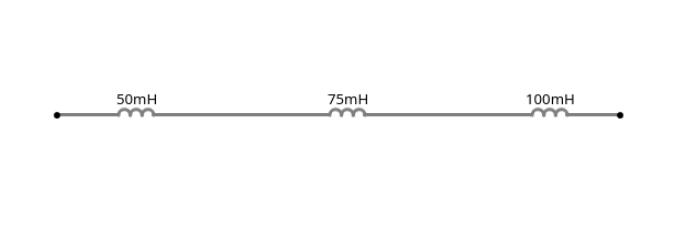
Fórmula para Inductores en Serie

Dado: L₁ = 50 mH, L₂ = 75 mH, L₃ = 100 mH

1. La fórmula para inductancias en serie es la suma simple de las inductancias:

\( L_{\text{total}} = L_1 + L_2 + L_3 \)

2. Sustituye los valores dados:

\( L_{\text{total}} = 50 \, \text{mH} + 75 \, \text{mH} + 100 \, \text{mH} \)

3. Calcula la suma:

\( L_{\text{total}} = 225 \, \text{mH} \)

Suma de Inductancias en Paralelo:

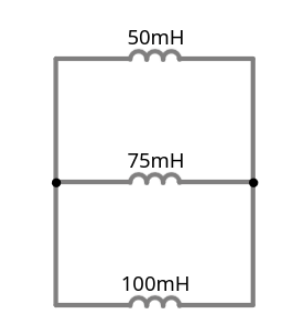
Fórmula para Inductores en Paralelo

Dado: L₁ = 50 mH, L₂ = 75 mH, L₃ = 100 mH

1. La fórmula para inductancias en paralelo involucra el uso del inverso de las inductancias:

\( \frac{1}{L_{\text{total}}} = \frac{1}{L_1} + \frac{1}{L_2} + \frac{1}{L_3} \)

2. Sustituye los valores dados:

\( \frac{1}{L_{\text{total}}} = \frac{1}{50 \, \text{mH}} + \frac{1}{75 \, \text{mH}} + \frac{1}{100 \, \text{mH}} \)

3. Calcula la suma de los inversos:

\( \frac{1}{L_{\text{total}}} = \frac{50 \cdot 75}{50 \cdot 75 \cdot 100} + \frac{50 \cdot 100}{50 \cdot 75 \cdot 100} + \frac{75 \cdot 100}{50 \cdot 75 \cdot 100} \, \text{H}^{-1} \)

\( \frac{1}{L_{\text{total}}} = \frac{3750}{50 \cdot 75 \cdot 100} + \frac{5000}{50 \cdot 75 \cdot 100} + \frac{7500}{50 \cdot 75 \cdot 100} \, \text{H}^{-1} \)

\( \frac{1}{L_{\text{total}}} = \frac{3750 + 5000 + 7500}{50 \cdot 75 \cdot 100} \, \text{H}^{-1} \)

\( \frac{1}{L_{\text{total}}} = \frac{16250}{50 \cdot 75 \cdot 100} \, \text{H}^{-1} \)

\( \frac{1}{L_{\text{total}}} = \frac{13}{300} \, \text{H}^{-1} \)

4. Toma el recíproco para encontrar \(L_{\text{total}}\):

\( L_{\text{total}} = \frac{1}{\frac{13}{300}} \, \text{mH} \)

\( L_{\text{total}} = \frac{300}{13} \, \text{mH} \)

\( L_{\text{total}} = \frac{300}{13} \, \text{mH} \approx 23.07 \, \text{mH} \)

Ley de Joule

La Ley de Joule es un principio en la física que establece la relación entre la energía eléctrica, la corriente eléctrica, la resistencia eléctrica y el calor generado en un conductor eléctrico. Fue formulada por el físico británico James Prescott Joule en la década de 1840 y es fundamental en la comprensión de cómo se comporta la electricidad en circuitos y cómo se transforma la energía eléctrica en otras formas de energía, como el calor.

La Ley de Joule establece que la cantidad de calor generado (\(Q\)) en un conductor eléctrico es directamente proporcional al cuadrado de la corriente (\(I\)) que fluye a través del conductor, a la resistencia (\(R\)) del conductor y al tiempo (\(t\)) durante el cual fluye la corriente. Matemáticamente, se expresa como:

\(Q = I^2 \cdot R \cdot t\)

Donde:

• \(Q\) es la cantidad de calor generada (en joules).
• \(I\) es la corriente que fluye a través del conductor (en amperios).
• \(R\) es la resistencia del conductor (en ohmios).
• \(t\) es el tiempo durante el cual fluye la corriente (en segundos).

Supongamos que tenemos: Q = \(2000 \, \text{J}\), I = \(5 \, \text{A}\) y t = \(2 \, \text{horas}\).

1J = 0.24 cal

La fórmula de la Ley de Joule para calcular la resistencia es:

\(R = \frac{Q}{I^2 \cdot t}\)

La fórmula para calcular la inductancia es:

\(I = \frac{Q}{t}\)

Primero, convirtamos el tiempo a segundos:

\(t = 2 \, \text{horas} = 2 \times 3600 \, \text{segundos} = 7200 \, \text{segundos}\)

Ahora, calculemos la resistencia:

\(R = \frac{2000 \, \text{J}}{(5 \, \text{A})^2 \cdot 7200 \, \text{segundos}}\)

\(R = 0.0111 \, \Omega\)

Por lo tanto, con los valores dados, la resistencia sería aproximadamente \(0.0111 \, \Omega\).

V = RI

Q = IVt

\(V = \frac{Q}{I \cdot t} = \frac{2000 \, \text{J}}{5 \, \text{A} \cdot 2 \, \text{horas}}\)

\(V = \frac{2000 \, \text{J}}{5 \, \text{A} \cdot 7200 \, \text{segundos}}\)

\(V = 0.0556 \, \text{V}\)

Ley de Coulomb

La Ley de Coulomb es un principio fundamental de la electrostática en la física, formulada por el científico Charles-Augustin de Coulomb. Esta ley establece que la fuerza eléctrica entre dos cargas puntuales es directamente proporcional al producto de sus magnitudes de carga y inversamente proporcional al cuadrado de la distancia entre ellas. En resumen, la Ley de Coulomb describe cómo las cargas eléctricas interactúan entre sí a través de fuerzas eléctricas, similar a cómo la gravedad afecta a las masas en la Ley de Gravitación Universal de Newton.

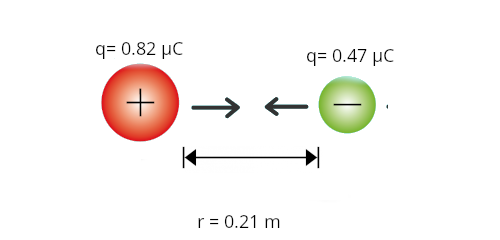
• Carga 1 (q₁) = 0.82 μC = 0.00000082 C
• Carga 2 (q₂) = 0.47 μC = 0.00000047 C
• Distancia (r) = 0.21 m
• Constante (K) = 9x10⁹ \( \frac{Nm^{2}}{C^{2}} \)

\( F = K\frac{q_{1}*q_{2}}{r^{2}} \)

\( F = (9x10^{9} \frac{Nm^{2}}{C^{2}}) \frac{0.82x10^{-6}C*0.47x10^{-6}C}{0.21m^{2}} \)

\( F = 0.079N \)

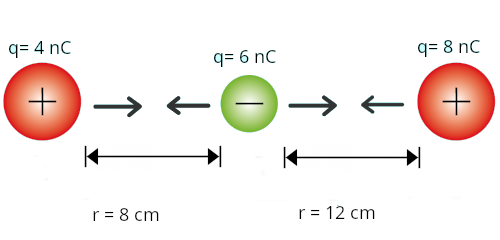
• Carga 1 (q₁) = 4 nC
• Carga 2 (q₂) = 6 nC
• Carga 3 (q₃) = 8 nC
• Distancia 1 (r) = 8 cm
• Distancia 2 (r) = 12 cm
• Constante (K) = 9x10⁹ \( \frac{Nm^{2}}{C^{2}} \)

Fuerza q₁ y q₂

\( F_{1} = K\frac{q_{1}*q_{2}}{r^{2}} \)

\( F_{1} = (9x10^{9} \frac{Nm^{2}}{C^{2}}) \frac{4x10^{-9}C*6x10^{-9}C}{0.08m^{2}} \)

\( F_{1} = 3.375x10^{-5}N \)

Fuerza q₂ y q₃

\( F_{2} = (9x10^{9} \frac{Nm^{2}}{C^{2}}) \frac{6x10^{-9}C*8x10^{-9}C}{0.12m^{2}} \)

\( F_{2} = 3x10^{-5}N \)

Fuerza Resultante

Para calcular la fuerza resultante, se tiene que tomar en cuenta que las fuerzas que actúan sobre q₂ van en sentidos contrarios y sobre el mismo eje. Por lo tanto, se tiene que realizar una suma de fuerzas de la siguiente manera:

Cuando la fuerza va hacia la derecha, se toma como una fuerza positiva; en caso contrario, tendrá signo negativo.

\( F_{R} = 3x10^{-5}N - 3.375x10^{-5}N \)

\( F_{R} = -3.75x10^{-6}N \)

\( F_{R} = 3.75x10^{-6}N \)

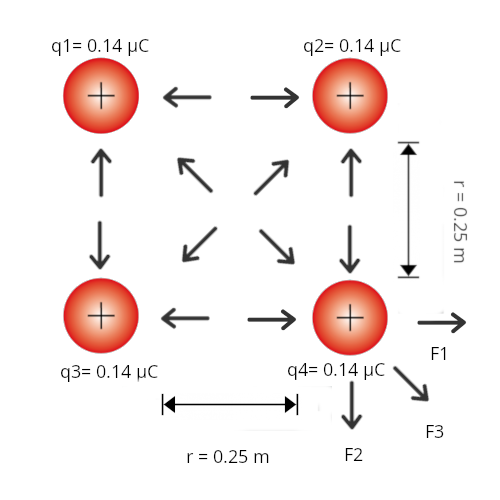
• Carga 1 (q₁) = 0.14 μC
• Carga 2 (q₂) = 0.14 μC
• Carga 3 (q₃) = 0.14 μC
• Carga 4 (q₄) = 0.14 μC
• Distancia (r) = 25 cm
• Constante (K) = 9x10⁹ \( \frac{Nm^{2}}{C^{2}} \)

Para este ejercicio, se analizará el valor de la carga para la carga inferior derecha, que será denominada como q₄.

Basándose en el gráfico que nos muestra cómo actúan las cargas entre sí, tenemos que existen 3 fuerzas actuando en diversos sentidos actuando con una fuerza de repulsión sobre q₄.

Fuerza q₄ y q₃

\( F_{1} = (9x10^{9} \frac{Nm^{2}}{C^{2}}) \frac{0.14x10^{-6}C*0.14x10^{-6}C}{0.25m^{2}} \)

\( F_{1} = 2.82x10^{-3}N (i) \)

La fuerza tiene dirección a lo largo del eje x.

Fuerza q₄ y q₂

\( F_{2} = -2.82x10^{-3}N (j) \)

La fuerza tiene dirección a lo largo del eje y.

Fuerza q₄ y q₁

r² = a² + b²

\(r^2 = 25^2 + 25^2 = 1250\)

\(r = \sqrt{1250} = 35.36\, \text{cm}\)

\( F_{3} = (9x10^{9} \frac{Nm^{2}}{C^{2}}) \frac{0.14x10^{-6}C*0.14x10^{-6}C}{0.35m^{2}} \)

\( F_{3} = 1.44x10^{-3}N (i, j) \)

\( F_{3} = 1.44x10^{-3} (Cos 45, Sen 45) \)

\( F_{3} = 1.018x10^{-3}N (i) - 1.018x10^{-3}N (j) \)

La fuerza F₃ actua en el eje x y.

Fuerza Resultante

\( F_{R} = 2.82x10^{-3}i - 2.82x10^{-3}j + 1.018x10^{-3}i - 1.018x10^{-3}j \)

\( F_{R} = 3.838x10^{-3}i - 3.838x10^{-3}j \)

\(F{R} = \sqrt{(3.838x10^{-3})^{2} + (-3.838x10^{-3})^{2}} \)

\(F{R} = \sqrt{2.94x10^{-5}} \)

\(F{R} = 5.42x10^{-3}N \)

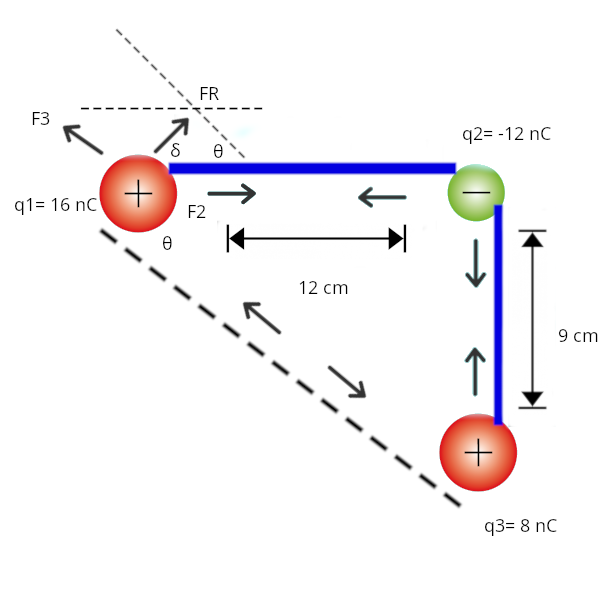
• Carga 1 (q₁) = 0.16 nC
• Carga 2 (q₂) = 0.12 nC
• Carga 3 (q₃) = 0.8 nC
• Distancia 1 (r) = 12 cm
• Distancia 2 (r) = 9 cm
• Constante (K) = 9x10⁹ \( \frac{Nm^{2}}{C^{2}} \)

Suponiendo que existen 3 cargas organizadas como se muestra en el esquema anterior. ¿Cuál sería la fuerza resultante que actúa sobre la carga q1 (la carga de la izquierda)?

En este ejercicio, vamos a hacer uso del método del paralelogramo para encontrar la fuerza resultante sobre q1.

\( F_{2} = (9x10^{9} \frac{Nm^{2}}{C^{2}}) \frac{16x10^{-9}C*-12x10^{-9}C}{0.12m^{2}} \)

\( F_{2} = 1.2x10^{-4}N \)

\(r^2 = 9^2 + 12^2 = 225\)

\(r = \sqrt{225} = 15\, \text{cm}\)

\( F_{3} = (9x10^{9} \frac{Nm^{2}}{C^{2}}) \frac{16x10^{-9}C*8x10^{-9}C}{0.15m^{2}} \)

\( F_{3} = 5.12x10^{-5}N \)

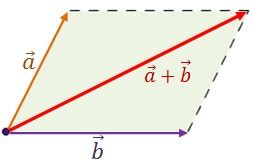
Ahora utilizaremos el método del paralelogramo para obtener el ángulo θ.

El método del paralelogramo se utiliza para sumar dos vectores usando regla del paralelogramo, y a menudo implica trabajar con ángulos.

tan θ = 9cm/12cm = 0.75

θ = arctan 0.75

θ = 36.87∘

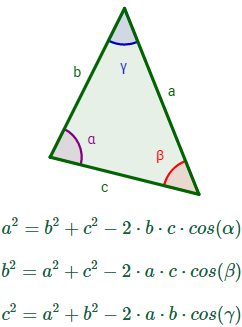
Por último, necesitamos aplicar el teorema del coseno para encontrar la fuerza resultante que actúa sobre q1.

\( F_{R}^{2} = (120x10^{-6})^{2} + (51.2x10^{-6})^{2} - 2(120x10^{-6})(51.2x10^{-6})cos36.87 \)

\( F_{R}^{2} = 7191.05x10^{-6}N^{2} \)

\( F_{R} = \sqrt{7191.05x10^{-6}} = 84.8x10^{-6} N \)

Usaremos el teorema del seno para poder obtener el ángulo dirección de nuestro vector resultante.

\( \frac{Sen \delta}{F_{3}} = \frac{Sen θ}{F_{R}} \)

\( \frac{Sen \delta}{51.2x10^{-6}} = \frac{Sen 36.87}{84.8x10^{-6}} \)

\( {Sen \delta} = \frac{Sen 36.87}{84.8x10^{-6}} * 51.2x10^{-6} = 0.36 \)

δ = arcsen 0.36 = 21.24∘

Mallas

La Ley de Voltajes de Kirchhoff (Ley de Mallas) establece que la suma algebraica de los voltajes en un circuito cerrado (malla) es igual a cero. Esto se deriva de la conservación de la energía.

\( \sum V_{\text{subida}} - \sum V_{\text{bajada}} = 0 \)

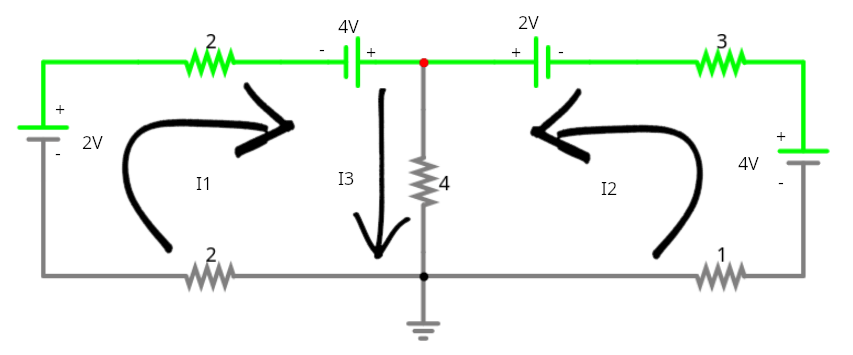
V = R*I

I₃= I₁ + I₂

Se calcula la suma de corrientes utilizando la ley de Ohm con los valores indicados por el circuito.

Malla 1:

2V + 4V = 2I₁ + 2I₁ + 4 (I₁+I₂)

6V = 2I₁ + 2I₁ + 4I₁+ 4I₂

6V = 8I₁ + 4I₂ ... ecuación (1)

Malla 2:

4V + 2V = 3I₂ + 1I₂ + 4 (I₁+I₂)

6V = 3I₂ + 1I₂ + 4I₁+ 4I₂

6V = 8I₂ + 4I₁ ... ecuación (2)

Igualación:

8I₁ + 4I₂ = 8I₂ + 4I₁

8I₁ - 4I₁ = 8I₂ - 4I₂

4I₁ = 4I₂

I₁ = I₂

Sustitución:

6V = 8I₁ + 4I₂

6V = 12I₁

I₁ = 6/12

I₁ = 0.5 Amp

Finalmente:

I₃= I₁ + I₂

I₃ = 0.5 Amp + 0.5 Amp

I₃ = 1 Amp

Mallas 2

Para el siguiente circuito, tenemos corrientes que van en sentidos contrarios, lo que afectará en los signos al realizar la sumatoria de voltajes, dependiendo de qué malla se esté analizando.

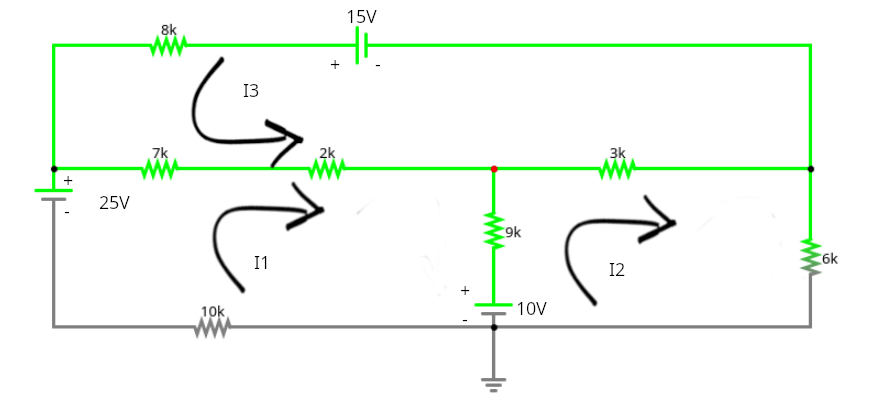
Suma de voltajes en las mallas. Se tiene que tener en cuenta la dirección de la corriente para realizar el análisis de forma correcta.

Malla 1:

25V - 10V = (7+2+9+10)I₁ + (7+2)I₃ - 9I₂

15V = 28I₁ - 9I₂ + 9I₃

Malla 2:

10V = (9+3+6)I₂ - 9I₁ + 3I₃

10V = -9I₁ + 18I₂ + 3I₃

Malla 3:

15V = (8+7+2+3)I₃ + (7+2)I₁ + 3I₂

15V = 9I₁ + 3I₂ + 20I₃

Como se está utilizando un circuito con un número mayor de mallas, es necesario usar un método de cálculo para sistemas 3x3.

Para resolver sistemas de ecuaciones con más variables y ecuaciones, se pueden utilizar matrices para realizar el cálculo. Por lo tanto, utilizaremos el método de determinantes en esta ocasión.

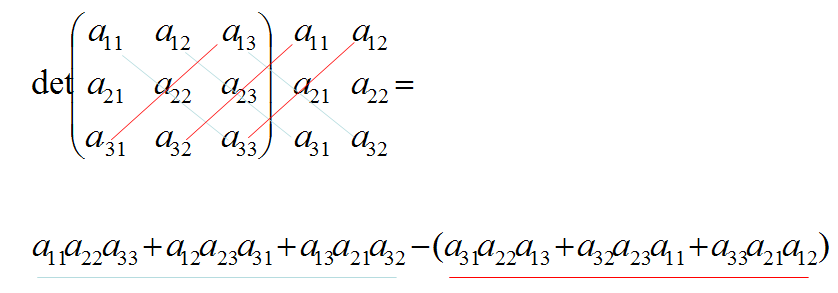
28I₁ - 9I₂ + 9I₃ = 15V

-9I₁ + 18I₂ + 3I₃ = 10V

9I₁ + 3I₂ + 20I₃ = 15V

Calculamos el determinante para la corriente 1.

Cálculo para DI₁:

DI₁ = (15*18*20) + (10*3*9) + (15*-9*3) - (10*-9*20) - (15*3*3) - (15*18*9)

DI₁ = (5400 + 270 - 405) - (-1800 + 135 + 2430)

DI₁ = 5265 - 765 = 4500

Calculamos el determinante para la corriente 2.

Cálculo para DI₂:

DI₂ = (28*10*20) + (-9*15*9) + (9*15*3) - (-9*15*20) - (28*15*3) - (9*10*9)

DI₂ = (5400 - 1215 + 405) - (-2700 + 1260 + 810)

DI₂ = 4790 + 630 = 5420

Calculamos el determinante para la corriente 3.

Cálculo para DI₃:

DI₃ = (28*18*15) + (-9*3*15) + (9*-9*10) - (-9*-9*15) - (28*3*10) - (9*18*15)

DI₃ = (7560 - 405 - 810) - (1215 + 840 + 2430)

DI₃ = 6345 - 4485 = 1860

Calculamos el determinante para la corriente.

Cálculo para DI:

DI = (28*18*20) + (-9*3*9) + (9*-9*3) - (-9*-9*20) - (28*3*3) - (9*18*9)

DI = (10080 - 243 - 243) - (1620 + 252 + 1458)

DI = 9594 - 3330 = 6264

Corrientes:

I₁ = 4500/6264 = 0.718mA

I₂ = 5420/6264 = 0.865mA

I₃ = 1860/6264 = 0.296mA

Potencia para la resistencia de 3k:

P_3k = I²R

I = I₂ + I ₃ = 0.865mA + 0.296mA = 1.161mA

W_3k = (1.161x10^-3)²(3000) = 4.04x10^-3W

Nodos

Las leyes de Kirchhoff son reglas fundamentales en circuitos eléctricos. La Ley de Corrientes de Kirchhoff (Ley de Nodos) establece que la suma de las corrientes que entran en un nodo es igual a la suma de las corrientes que salen. Esto se basa en la conservación de la carga eléctrica.

\( \sum I_{\text{entrante}} = \sum I_{\text{saliente}} \)

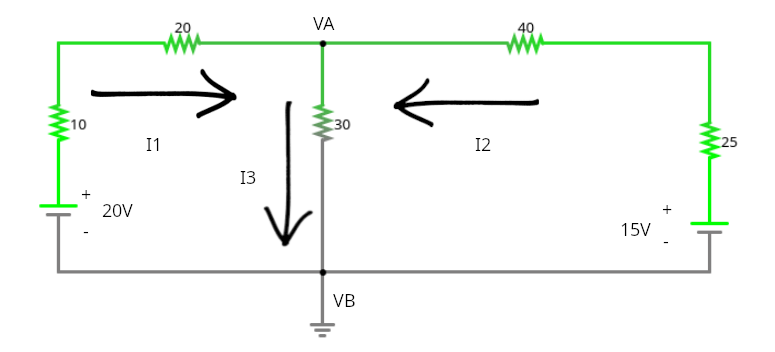
Al tener la polaridad de las dos fuentes conectadas de tal forma, tenemos que la corriente I1 e I2 entran al nodo A, dando como resultado una corriente de salida I3. El nodo B, en la parte inferior al estar en contacto con la polaridad negativa, se toma como tierra; por lo tanto, no se calcula.

Nodo A:

I₁ + I₂ = I₃

20 = I₁(10+20) + VA

15 = I₂(40+25) + VA

VA = I₃(30) + VB

I₁ = \( \frac{20 - VA}{10 + 20} \)

I₂ = \( \frac{15 - VA}{40 + 25} \)

I₃ = \( \frac{VA - VB}{30} \)

\( \frac{20 - VA}{10 + 20} + \frac{15 - VA}{40 + 25} = \frac{VA - VB}{30} \)

\( \frac{20 - VA}{30} + \frac{15 - VA}{65} = \frac{VA - VB}{30} \)

\( \frac{20 - VA}{30} + \frac{15 - VA}{65} = \frac{VA - VB}{30} \)

\( \frac{20}{30} - \frac{VA}{30} + \frac{15}{65} - \frac{VA}{65} = \frac{VA}{30} \)

\( \frac{20}{30} + \frac{15}{65} = \frac{VA}{30} + \frac{VA}{30} + \frac{VA}{65} \)

El mínimo común múltiplo de 30 y 65 es 390.

Se divide el mínimo común múltiplo por el denominador y se multiplica el numerador a cada fracción para obtener el numerador de la fracción final.

\( \frac{260 + 90}{390} = \frac{13VA + 13VA + 6VA}{390} \)

350 = 32VA

\( \frac{350}{32} = VA \)

VA = 10.93 V

Corrientes:

I₁ = \( \frac{20 - VA}{30} \)

I₁ = \( \frac{(20 - 10.93)V}{30} \)

I₁ = 0.302 Amp

I₂ = \( \frac{15 - VA}{65} \)

I₂ = \( \frac{(15 - 10.93)V}{65} \)

I₂ = 0.062 Amp

I₃ = \( \frac{VA}{30} \)

I₃ = \( \frac{10.93V}{30} \)

I₃ = 0.364 Amp

Voltaje en R2:

V_R2 = I₂ * 25

V_R2 = 0.062 * 25

V_R2 = 1.55 V

Potencia en R1:

P_R1 = I₁² * 20

P_R1 = (0.302)² (20)

P_R1 = 1.82 W

Nodos 2

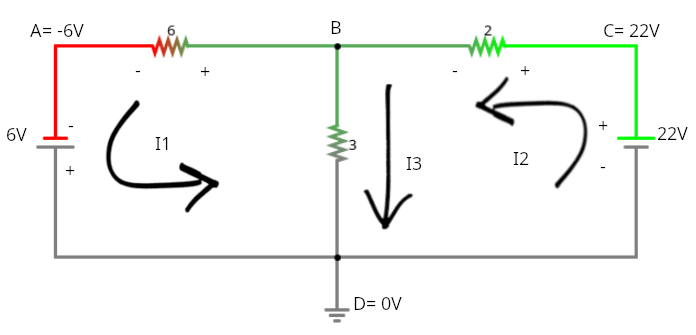
En el siguiente circuito, las corrientes que fluyen van en sentido contrario con respecto al nodo B, ya que las fuentes de voltaje están conectadas en sentidos contrarios.

La ley de nodos dice que las corrientes que entran al nodo se toman como positivas y las que salen como negativas. Por lo tanto, nos queda la ecuación de corrientes de la siguiente forma:

-I₁ + I₂ + (-I₃) = 0

-I₁ + I₂ - I₃ = 0

-VA = I₁(R1) - VB

VC = I₂(R2) + VB

VB = I₃(R3) + VD

Para calcular la intensidad, sirve tomar como referencia el voltaje mayor como positivo en la ecuación y el voltaje de menor valor como negativo.

I₁ = \( \frac{VB - VA}{R1} \) = \( \frac{VB - (-6V)}{6} \)

I₁ = \( \frac{VB}{6} \) + \( \frac{6V}{6} \) = \( \frac{VB}{6} \) + 1A

I₂ = \( \frac{VC - VB}{R2} \) = \( \frac{22V - VB}{2} \)

I₂ = \( \frac{22V}{2} \) - \( \frac{VB}{2} \) = 11A - \( \frac{VB}{2} \)

I₃ = \( \frac{VB - VD}{R3} \) = \( \frac{VB - 0V}{3} \)

I₃ = \( \frac{VB}{3} \) - 0V = \( \frac{VB}{3} \)

Suma de corrientes:

- (\( \frac{VB}{6} \) + 1A) + (11A - \( \frac{VB}{2} \)) - (\( \frac{VB}{3} \)) = 0

10A - \( \frac{VB}{6} \) - \( \frac{3VB}{6} \) - \( \frac{2VB}{6} \) = 0

10A - \( \frac{6VB}{6} \) = 0

10A = \( \frac{6VB}{6} \)

10A * 6 = 6VB

\( \frac{60A}{6} \) = VB

VB = 10V

I₁ = \( \frac{10}{6} \) + 1A = 2.66A

I₂ = 11A - \( \frac{10}{2} \) = 6A

I₃ = \( \frac{10}{3} \) = 3.33A

Circuito RLC en Alterna

Supongamos que tenemos el siguiente circuito:

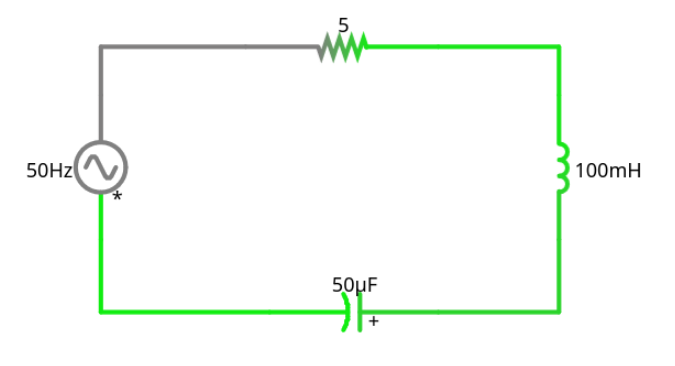
Cálculo para números reales

• Voltaje (V) = 10 V
• Frecuencia (F) = 50 Hz
• Resistencia (R) = 5Ω
• Inductancia (L) = 0.1 H
• Capacitancia (C) = 50 μF = 0.00005 F

Para calcular la corriente en el circuito en serie, necesitamos conocer la fuente de voltaje o la corriente inicial en el inductor o el capacitor. Supongamos que conectamos una fuente de voltaje de 10V a este circuito.

Para calcular la corriente en el circuito, podemos utilizar la Ley de Ohm. La impedancia total (Z) de un circuito en serie con resistancia (R), inductancia (L) y capacitancia (C) es la suma de las impedancias individuales:

Z = R + jωL + 1/(jωC)

Donde:

j = Unidad imaginaria (j = √(-1))

ω = Frecuencia angular (ω = 2πf, donde f es la frecuencia en Hz)

Supongamos una frecuencia de 50 Hz (esto implica ω = 2π * 50 Hz = 100π rad/s).

Ahora, podemos calcular la impedancia total Z y luego la corriente (I) usando la Ley de Ohm:

Z = 5Ω + j * 100π * 0.1H + 1/(j * 100π * 50μF)

Calculamos los valores en la forma rectangular (real + imaginario * j) para Z:

Z = 5 + j31.42 + j63.66

Reactancias:

• Reactancia inductiva (XL):

XL = 2π * F * L = 2 * π * 50 * 0.1 = 31.42

• Reactancia capacitiva (XC):

XC = 1 / (2π * F * C) = 1 / (2 * π * 50 * 0.00005) ≈ 63.66

En este circuito, la reactancia capacitiva es mayor que la reactancia inductiva:

XC > XL

Impedancia total (Z):

Z = √(R² + (XC - XL)²) = √(5² + (63.66 - 31.42)²) ≈ 32.62

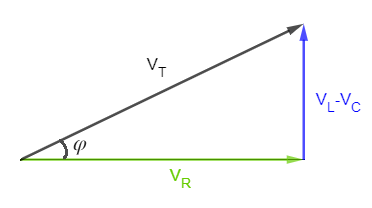
Ahora podemos calcular la corriente I utilizando la Ley de Ohm:

I = V / Z

Corriente total (I): I = V / Z = 10 / 32.62 ≈ 0.31 A

Voltajes:

• Voltaje en R (VR):

VR = I * R = 0.31 * 5 ≈ 1.55

• Voltaje en XL (VXL):

VXL = I * XL = 0.31 * 31.42 ≈ 9.74

• Voltaje en XC (VXC):

VXC = I * XC = 0.31 * 63.66 ≈ 19.66

Triángulo de Potencias:

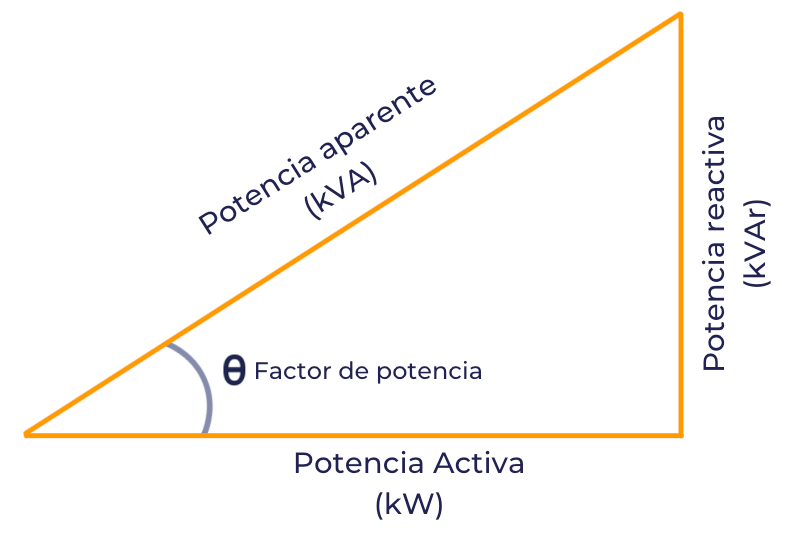
Obtenemos el ángulo del triangulo de impedancias:

Ángulo entre Z y R (ϕ_impedancia):

ϕ_impedancia = arccos(R / Z) = arccos(5 / 32.62) ≈ 81.18∘

Potencia aparente (S):

S = V * I = 10 * 0.31

S ≈ 3.1 VA

Potencia reactiva (Q):

Q = V * I * sin(ϕ_impedancia)

Q = 10 * 0.31 * sin(81.18) ≈ 3.1 VAR

Potencia activa (P):

P = V * I * cos(ϕ_impedancia)

P = 10 * 0.31 * cos(81.18) ≈ 0.4753 W

Cálculo por números complejos

Dado que ω = 2π × 50 rad/s y j es la unidad imaginaria (j^2 = -1), la impedancia total Z se calcula de la siguiente manera:

Z = R + j(ωL - 1/(ωC))

Calculamos Z:

Z = 5 + j(2π × 50 × 0.1 - 1/(2π × 50 × 0.00005))

Z = 5 + j(31.42 - 63.66)

Z = 5 - 32.24j Ω

Se necesita hacer uso de la calculadora para realizar la conversión entre números polares y reales, ya que el cálculo de la conversión es largo.

En números polares:

Z = 32.625Ω ∠−81.238∘

La corriente total I se calcula mediante I = V/Z:

I = (10 ∠0∘)/(32.625Ω ∠−81.238∘) ≈ 0.3065 ∠81.238∘ Amp

• Voltaje en la resistencia:

VR = I × R ≈ 5 * 0.3065 ∠81.238∘

VR ≈ 1.53 ∠81.238∘ V

La inductancia al ser un número imaginario positivo, tiene 90 grados.

• Voltaje en la inductancia:

VXL = I × ωL = 31.42 ∠90∘ * 0.3065 ∠81.238∘

VXL ≈ 9.63 ∠171.238∘ V

La capacitancia al ser un número imaginario negativo, tiene -90 grados.

• Voltaje en el capacitor:

VXC = I × 1/(ωC) = 63.66 ∠-90∘ * 0.3065 ∠81.238∘

VXC ≈ 19.51 ∠-8.762∘ V

La potencia aparente S = VI se descompone en potencia activa P y potencia reactiva Q, utilizando el ángulo θ:

S = 10 ∠0∘ × (0.3065 ∠81.238∘)

S = 3.065 ∠81.238∘ VA ≈ 0.467 + 3.03j

La potencia activa es la parte real y la imaginaria la potencia reactiva.

Nodos en Alterna

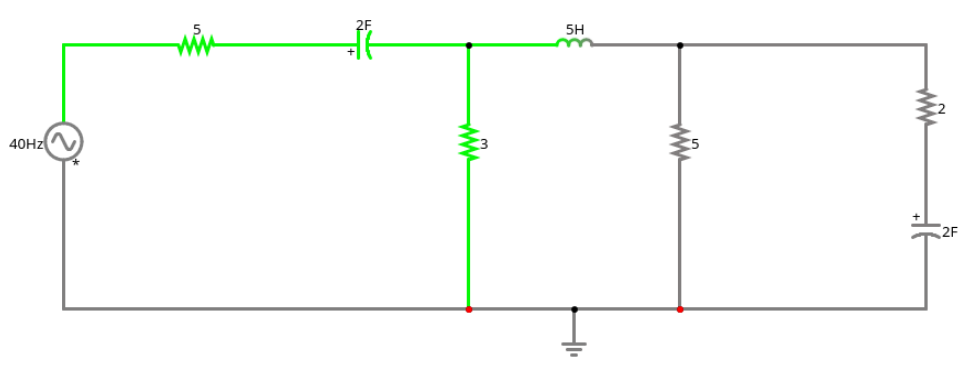
• Fuente (V) = 10 ∠30∘ V
• Voltaje 1 (V) = 3.02 ∠65.2∘ V
• Voltaje 2 (V) = 1.34 ∠-31.3∘ V
• Corriente (I_{10 ∠30∘}) = 1.44 ∠38.8∘ V

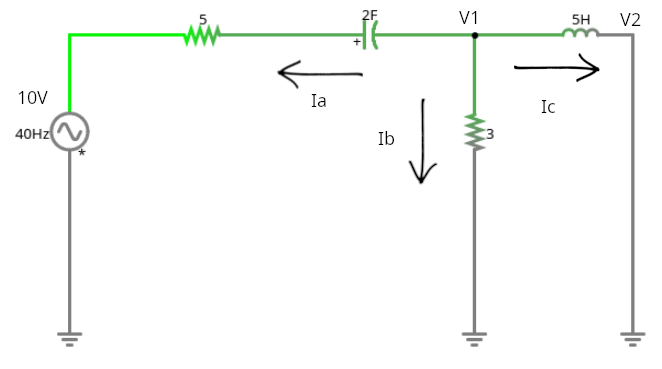
V₁ = (5 - j2)I_a + 10 ∠30∘

I_a = \( \frac{V_{1} - 10 ∠30^\circ}{5 - j2} \)

V₁ = 3I_b => I_b = \( \frac{V_{1}}{3} \)

V₁ = j5I_c + V₂

I_c = \( \frac{V_{1} - V_{2}}{j5} \)

Aplicamos L.K.I. al nodo 1:

I_a + I_b + I_c = 0

\( \frac{V_{1} - 10 ∠30^\circ}{5 - j2} \) + \( \frac{V_{1}}{3} \) + \( \frac{V_{1} - V{2}}{j5} \) = 0

\( (\frac{1}{5 - j2} + \frac{1}{3} + \frac{1}{j5})V_{1} \) - \( (\frac{1}{j5})V_{2} \) = \( \frac{10 ∠30^\circ}{5 - j2} \)

\( (\frac{1}{5.385 ∠-21.8^\circ} + 0.333 - j0.2)V_{1} \) + (j0.2)V₂ = \( \frac{10 ∠30^\circ}{5.385 ∠-21.8^\circ} \)

\( (0.1857 ∠21.8^\circ + 0.333 - j0.2)V_{1} \) + \( (j0.2)V_{2} \) = \( 1.875 ∠51.8^\circ \)

\( (0.1724 - j0.069 + 0.333 - j0.2)V_{1} \) + \( (j0.2)V_{2} \) = \( 1.875 ∠51.8^\circ \)

\( (0.5054 - j0.131)V_{1} \) + \( (j0.2)V_{2} \) = \( 1.875 ∠51.8^\circ \)

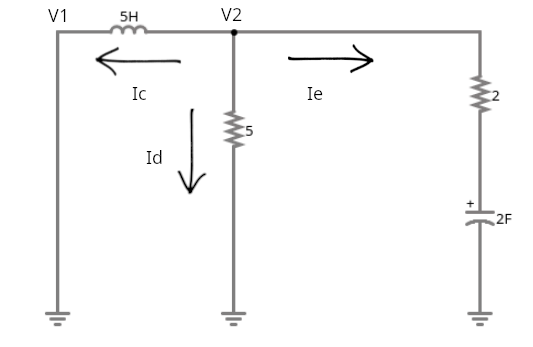
V₂ = j5I_c + V₁

I_c = \( \frac{V_{2} - V_{1}}{j5} \)

V₂ = 5I_d => I_d = \( \frac{V_{2}}{5} \)

I_e = \( \frac{V_{2}}{2 - j2} \)

Aplicamos L.K.I. al nodo 2:

I_c + I_d + I_e = 0

\( \frac{V_{2} - V_{1}}{j5} \) + \( \frac{V_{2}}{5} \) + \( \frac{V_{2}}{2 - j2} \) = 0

\( (\frac{-1}{j5})V_{1} \) + \( (\frac{1}{j5} + \frac{1}{5} + \frac{1}{2 - j2})V_{2} \) = 0

\( (j0.2)V_{1} \) + \( (-j0.2 + 0.2 + \frac{1}{2.8284 ∠-45^\circ})V_{2} \) = 0

\( (j0.2)V_{1} \) + \( (-j0.2 + 0.2 + 0.3536 ∠45^\circ )V_{2} \) = 0

\( (j0.2)V_{1} \) + \( (-j0.2 + 0.2 + 0.25 + j0.25)V_{2} \) = 0

\( (j0.2)V_{1} \) + \( (0.45 + j0.05)V_{2} \) = 0

Se realiza una multiplicación matricial considerando las ecuaciones de los nodos 1 y 2, así como los voltajes 1 y 2 correspondientes a cada nodo.

Se sustituyen los valores del voltaje 2 en las dos ecuaciones con el resultado de ambas ecuaciones.

V₂ = \( \frac{-(j0.2)(1.875 ∠51.8^\circ)}{(0.5054 - j0.131)(0.45 + j0.05) - (j0.2)(j0.2)} \)

V₂ = \( \frac{(0.2 ∠-90^\circ)(1.875 ∠51.8^\circ)}{(0.22743 + j0.0253 - j0.059 + 0.0066) + 0.04} \)

V₂ = \( \frac{0.375 ∠-38.2^\circ}{0.27403 - j0.0337} \)

V₂ = \( \frac{0.375 ∠-38.2^\circ}{0.2761 ∠-7.01^\circ} \)

V₂ = \( 1.358 ∠-31.19^\circ \)

Se sustituyen los valores del voltaje 1 en las dos ecuaciones con el resultado de ambas ecuaciones.

V₁ = \( \frac{(1.875 ∠51.8^\circ)(0.45 + j0.05)}{(0.5054 - j0.131)(0.45 + j0.05) - (j0.2)(j0.2)} \)

V₁ = \( \frac{(1.875 ∠51.8^\circ)(0.4528 ∠6.34^\circ)}{0.27403 - j0.0337} \)

V₁ = \( \frac{0.849 ∠58.14^\circ}{0.2761 ∠-7.01^\circ} \)

V₁ = \( 3.075 ∠65.15^\circ \)

I_a = \( \frac{V_{1} - 10 ∠30^\circ}{5 - j2} \)

I_a = \( \frac{3.075 ∠65.15^\circ - 10 ∠30^\circ}{5 - j2} \)

I_a = \( \frac{1.3 + j2.8 - 8.66 -j5}{5 - j2} \)

I_a = \( \frac{-7.36 -j2.2}{5 - j2} \) = \( \frac{-7.68 ∠16.64^\circ}{5.38 ∠-21.801^\circ} \)

I_a = -1.428 ∠38.44∘

I_a = -I_{10 ∠30∘}

I_{10 ∠30∘} = 1.428 ∠38.44∘

Conclusión

Recuerda que estos cálculos se basan en valores inventados para los componentes del circuito. En una aplicación práctica, estos valores pueden variar y afectar los resultados.