Conceptos clave del Deep Learning

El mundo del Deep Learning puede parecer complejo, pero detrás de su apariencia hay conceptos fundamentales que son esenciales para entender cómo las máquinas aprenden y procesan información. Aquí, te sumergiremos más profundamente en estos conceptos, proporcionando explicaciones detalladas y ejemplos sencillos:

Pesos

Los pesos (weights) son valores numéricos asignados a las conexiones entre las neuronas en una red neuronal. Cada conexión entre dos neuronas tiene un peso asociado. Estos pesos determinan la influencia relativa de las entradas en el cálculo de la salida de una neurona. Cuando una señal se propaga a través de la red neuronal, se multiplica por los pesos correspondientes en las conexiones.

Imagina que estás entrenando una red neuronal para reconocer dígitos escritos a mano. Cada peso puede verse como una medida de cuán importante es cierta característica (como la curva de un dígito) para tomar una decisión sobre el número representado en la imagen. Durante el entrenamiento, los pesos se ajustan para que la red aprenda a dar más peso a las características relevantes y menos peso a las que no lo son.

Perceptrón: La Unidad Básica

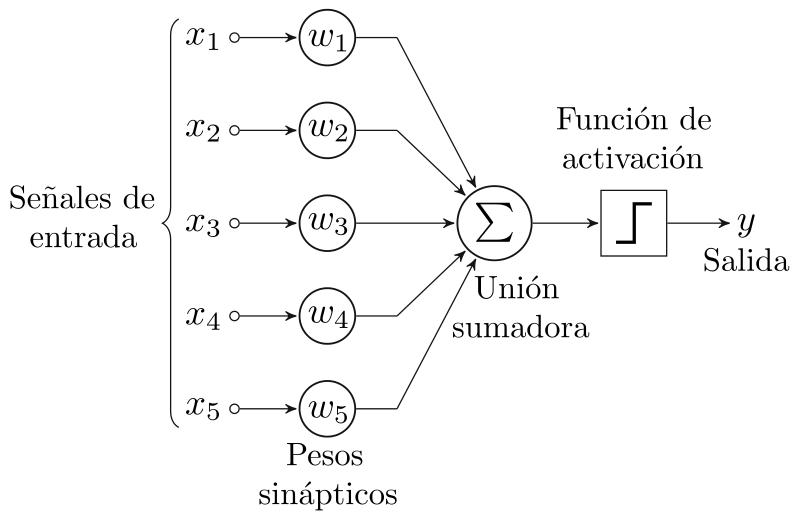
El perceptrón es como un pequeño ladrillo en la construcción de un edificio de inteligencia artificial. Piensa en él como una neurona artificial que recibe entradas, las multiplica por ciertos pesos y produce una salida. Por ejemplo, si estuviéramos enseñando a una red neuronal a diferenciar entre manzanas y naranjas, un perceptrón podría evaluar características como color y forma para hacer una predicción.

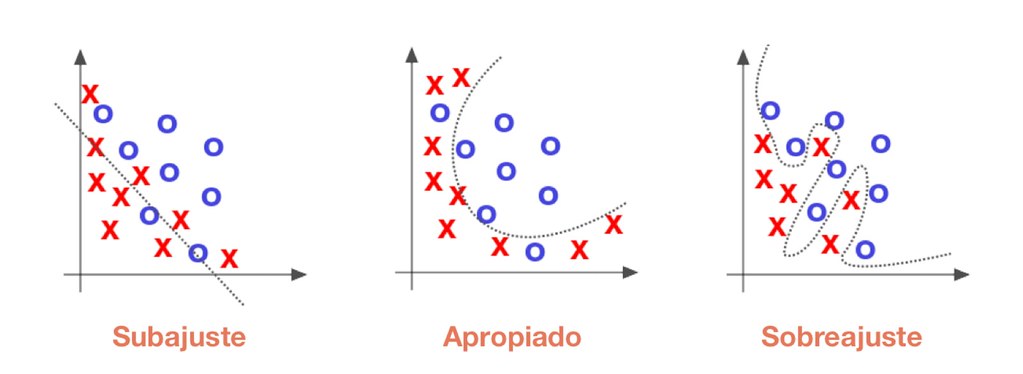
Sobreajuste y Subajuste: Equilibrio Delicado

El sobreajuste se da cuando un modelo se aprende de memoria los datos de entrenamiento, pero lucha para generalizar a datos nuevos. Imagina que estás aprendiendo matemáticas y memorizas respuestas en lugar de entender los conceptos. El subajuste, en cambio, ocurre cuando un modelo es demasiado simple para capturar patrones complejos. Sería como usar solo sumas y restas para resolver ecuaciones cuadráticas.

Bias y Varianza: Balance Fundamental

Los sesgos o bias son valores que se añaden a la suma ponderada de las entradas de una neurona antes de que pase por una función de activación. Pueden considerarse como una especie de "umbral" que controla cuándo y cómo se activará la neurona.

En el contexto de modelos de aprendizaje automático, incluido el aprendizaje profundo, el sesgo (bias) se refiere a la diferencia entre las predicciones del modelo y los valores reales o esperados. Un modelo con un alto sesgo tiende a simplificar demasiado las relaciones en los datos y puede no ser lo suficientemente flexible para capturar patrones complejos. Por otro lado, un modelo con bajo sesgo puede ajustarse mejor a los datos de entrenamiento, pero podría correr el riesgo de sobreajuste. En resumen, el sesgo se refiere a cómo de cerca están las predicciones de un modelo del valor verdadero o deseado.

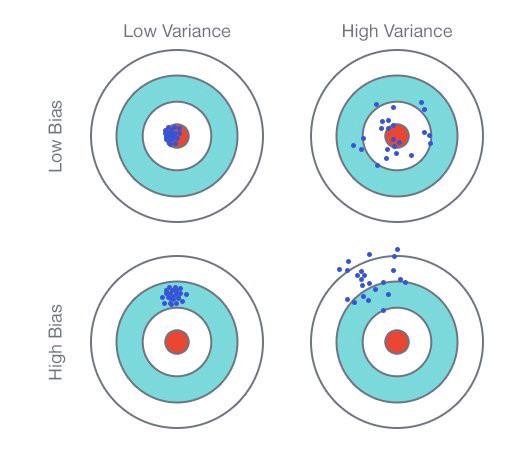
Imagina que estás intentando dar en el blanco en un juego de dardos. Si siempre lanzas tus dardos cerca de un solo punto, tienes alto bias, es decir, no consideras suficientes variables. Por otro lado, si lanzas dardos dispersos por toda la diana, tienes alta varianza, es decir, estás siendo muy sensible a pequeñas diferencias. El reto es encontrar un equilibrio entre estas dos para hacer predicciones precisas. Es esencial encontrar un equilibrio para que el modelo no simplifique en exceso ni capture ruido innecesario.

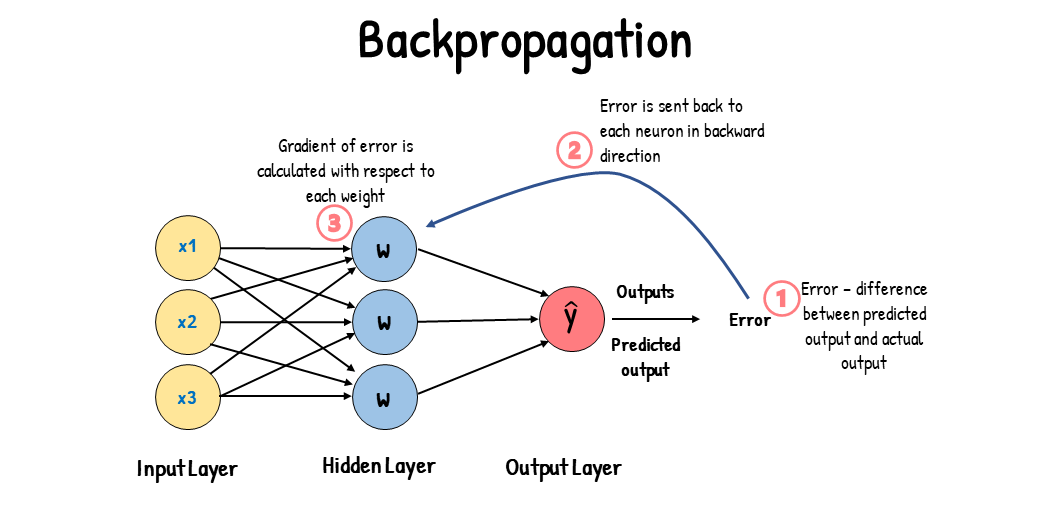
Backpropagation: Aprendizaje Detrás de Escena

Es una técnica que ajusta los pesos y los sesgos de las conexiones entre las neuronas en función del error calculado entre las predicciones del modelo y los valores reales de salida. En esencia, es como enseñarle a la red neuronal a mejorar su rendimiento y a aprender de sus errores.

Imagina que estás enseñando a alguien a identificar diferentes tipos de flores en función de sus características. Al principio, pueden cometer errores al identificarlas, pero con cada error, les das retroalimentación sobre lo que hicieron mal. Gradualmente, ajustan su enfoque y se vuelven más precisos en sus predicciones.

En términos más técnicos, el Backpropagation implica dos etapas principales:

Forward Pass (Pase hacia adelante): Durante esta fase, los datos de entrada se propagan a través de la red neuronal, pasando por las capas de neuronas y las funciones de activación. Esto da como resultado una predicción.
Cálculo de Gradientes: Una vez que tenemos una predicción, calculamos el error al compararla con el valor real. Luego, calculamos cómo pequeños cambios en los pesos y sesgos de las conexiones afectarían el error. Esta información se utiliza para ajustar los pesos y sesgos en la dirección que reduce el error.

El proceso de Backpropagation se repite a lo largo de múltiples iteraciones (épocas) de entrenamiento. Cada vez que los datos pasan a través de la red, los pesos se ajustan para mejorar la precisión de las predicciones. Con el tiempo, esto permite que la red neuronal aprenda patrones complejos en los datos y genere predicciones más precisas.

El Backpropagation es como el maestro que guía a la red neuronal para que mejore con cada intento. A través de ajustes sistemáticos en los pesos y sesgos, la red aprende a hacer predicciones más precisas y a capturar relaciones importantes en los datos, lo que la convierte en una herramienta poderosa para tareas como reconocimiento de patrones, clasificación y más.

Imagina enseñar a un perro nuevos trucos. Comienzas recompensándolo cuando hace algo bien y corriges cuando se equivoca. Backpropagation hace algo similar. Al calcular la diferencia entre las predicciones y las respuestas reales, ajusta los pesos en la red para mejorar el rendimiento en futuras iteraciones.

Desvanecimiento del Gradiente: Problema de Entrenamiento

El Desvanecimiento del Gradiente (Gradient Vanishing en inglés) es un problema que puede ocurrir durante el entrenamiento de redes neuronales profundas, particularmente en aquellas que tienen muchas capas. Se refiere a la disminución gradual de los gradientes a medida que se propagan hacia atrás a través de las capas durante el proceso de Backpropagation.

Los gradientes son valores que indican la dirección y la magnitud en la que deben ajustarse los pesos y sesgos de las conexiones entre las neuronas para minimizar el error. En un entrenamiento exitoso, los gradientes deben ser lo suficientemente grandes para impulsar ajustes significativos en los pesos y sesgos, lo que permite que la red neuronal aprenda con eficacia.

Sin embargo, en redes neuronales profundas, especialmente aquellas con muchas capas, los gradientes pueden volverse muy pequeños a medida que se propagan hacia capas más profundas. Esto puede resultar en que los pesos de las capas anteriores no se ajusten significativamente, lo que ralentiza o incluso detiene el proceso de aprendizaje en esas capas. Como resultado, las capas más profundas pueden tener dificultades para capturar patrones y aprender relaciones en los datos.

El Desvanecimiento del Gradiente puede ser problemático porque las capas más profundas de una red neuronal profunda a menudo son las que se supone que deben aprender características de alto nivel y relaciones más complejas en los datos. Si los gradientes se desvanecen, estas capas no podrán capturar correctamente la información necesaria para realizar tareas más avanzadas.

Una solución para mitigar el Desvanecimiento del Gradiente es el uso de funciones de activación no lineales que evitan que los gradientes se desvanezcan tan rápidamente. Además, arquitecturas de redes neuronales más modernas, como las redes neuronales recurrentes (RNN) y las redes neuronales convolucionales (CNN), han demostrado ser más resistentes a este problema debido a su estructura y conexiones especiales.

El Desvanecimiento del Gradiente es un desafío que puede afectar la capacidad de las redes neuronales profundas para aprender y generalizar patrones en datos complejos. Las estrategias para enfrentar este problema son esenciales para construir redes neuronales profundas eficaces y exitosas.

Supón que estás dando pasos en una montaña, pero cada paso es más pequeño que el anterior. Eventualmente, te detendrás sin alcanzar la cima. En Deep Learning, cuando los gradientes se vuelven muy pequeños, el modelo deja de aprender. Es importante manejar este problema para que el aprendizaje sea efectivo en todas las capas.

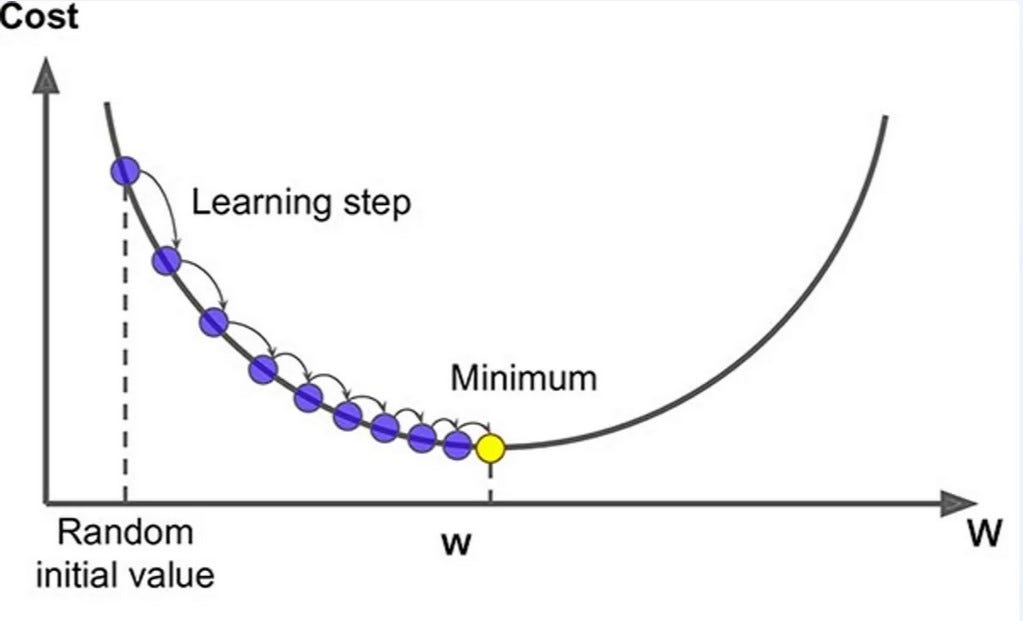
Función de Pérdida (Loss) y Función de Error: Evaluar el Rendimiento

La "Función de Pérdida" (Loss Function en inglés) y la "Función de Error" (Error Function en inglés) son conceptos relacionados pero diferentes en el contexto del entrenamiento de modelos en el aprendizaje automático y el Deep Learning.

⭕ Función de Pérdida (Loss Function): La Función de Pérdida es una medida que cuantifica cuán bien o mal está realizando un modelo sus predicciones en comparación con los valores reales. En otras palabras, mide la discrepancia entre las salidas pronosticadas por el modelo y las salidas reales. La Función de Pérdida es esencial para entrenar modelos ya que proporciona una guía para ajustar los parámetros del modelo (como pesos y sesgos) durante el proceso de entrenamiento.

Ejemplo: Si estamos entrenando un modelo para predecir el precio de una casa en función de sus características, la Función de Pérdida podría medir la diferencia entre las predicciones del modelo y los precios reales de las casas.

⭕ Función de Error (Error Function): La Función de Error también se refiere a la medida de cuán incorrectas son las predicciones del modelo, pero a menudo se usa de manera más general para describir cualquier métrica que mida el rendimiento de un modelo. En algunos casos, puede ser sinónimo de la Función de Pérdida. Sin embargo, en otros contextos, la Función de Error podría referirse a una métrica de rendimiento más amplia, como la precisión, el error cuadrático medio o cualquier otra medida que evalúe el rendimiento global del modelo.

Ejemplo: En un problema de clasificación de imágenes, la Función de Error podría ser la tasa de clasificación incorrecta de todas las imágenes de prueba.

La función de pérdida (Loss Function) es una medida específica que cuantifica la discrepancia entre las predicciones y los valores reales, y se utiliza para ajustar los parámetros del modelo durante el entrenamiento. La Función de Error (Error Function), por otro lado, se refiere más ampliamente a cualquier métrica que evalúa el rendimiento general del modelo. Ambas son esenciales para evaluar y mejorar la eficacia de los modelos de aprendizaje automático y Deep Learning.

La función de pérdida es como un juez que evalúa cuán cerca estás de tu objetivo en un juego. El juego podría ser predecir el precio de una casa en función de su tamaño y ubicación. La función de pérdida mide cuánto te desvías del precio real, y la función de error es la suma total de esas desviaciones.

Selección de Características y Reducción de Dimensiones

La "Selección de Características" y la "Reducción de Dimensiones" son dos técnicas comunes en el campo del aprendizaje automático y la minería de datos que se utilizan para mejorar el rendimiento y la eficiencia de los modelos, así como para comprender y visualizar conjuntos de datos complejos. Ambas técnicas se aplican a los datos antes de alimentarlos a los algoritmos de aprendizaje automático.

⭕ Selección de Características: La selección de características se refiere al proceso de elegir un subconjunto relevante de características (variables) de un conjunto de datos original más grande. El objetivo es eliminar las características que pueden ser redundantes, irrelevantes o incluso perjudiciales para el rendimiento del modelo. Al seleccionar características adecuadas, se puede mejorar la precisión del modelo, reducir el tiempo de entrenamiento y evitar el sobreajuste.

La selección de características puede ser realizada manualmente por expertos en el dominio o de manera automática utilizando algoritmos específicos que evalúan la importancia y relevancia de cada característica en relación con la variable objetivo.

⭕ Reducción de Dimensiones: La reducción de dimensiones es un enfoque más avanzado que busca transformar los datos originales en un nuevo espacio de menor dimensión mientras se conserva la mayor cantidad posible de información relevante. Esto es especialmente útil cuando se enfrenta a conjuntos de datos con muchas características, ya que la alta dimensionalidad puede llevar a problemas de "maldición de la dimensionalidad" y dificultar el procesamiento y la interpretación.

Una técnica común para reducir la dimensión es el Análisis de Componentes Principales (PCA, por sus siglas en inglés), que busca proyectar los datos originales en un nuevo conjunto de ejes ortogonales (componentes principales) que capturan la mayor variabilidad. Otras técnicas, como el Análisis Discriminante Lineal (LDA) o métodos de factorización de matriz, también se utilizan para reducir la dimensión y preservar las relaciones relevantes en los datos.

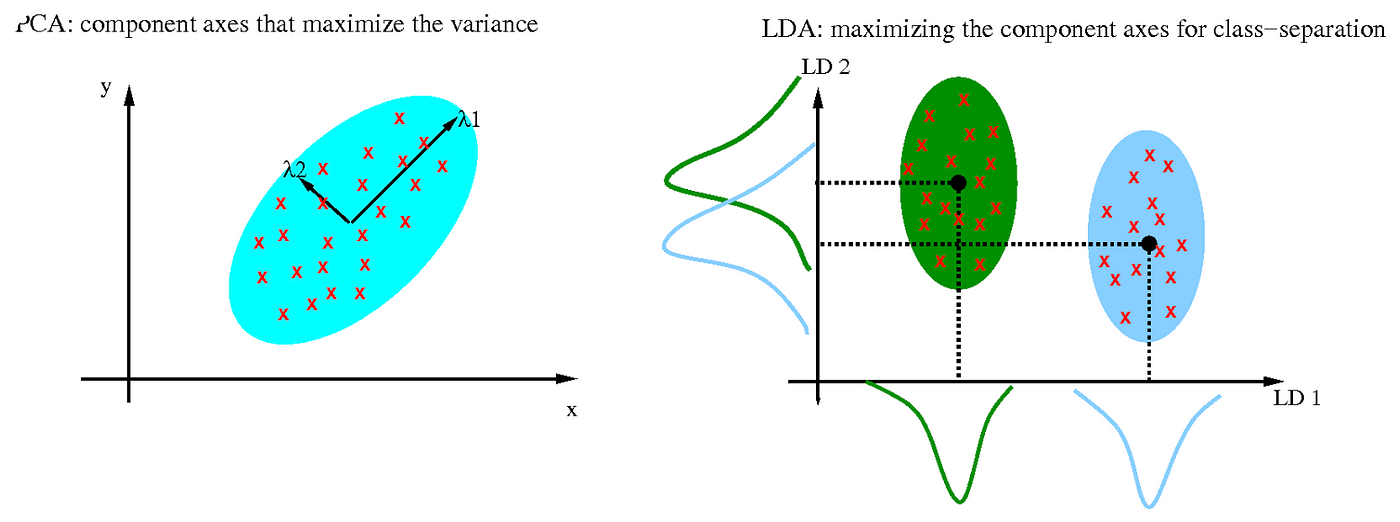
Tanto la selección de características como la reducción de dimensiones tienen como objetivo mejorar la calidad de los datos utilizados para el aprendizaje automático y la minería de datos. La selección de características se centra en la elección de las características más relevantes, mientras que la reducción de dimensiones busca representar los datos en un espacio de menor dimensión para facilitar el procesamiento y la interpretación. Ambas técnicas son herramientas valiosas para abordar desafíos asociados con la complejidad y la cantidad de datos en la actualidad.

La selección de características es como elegir las cartas correctas en un juego de cartas para ganar. Reducción de dimensiones es como usar cartas más grandes pero más poderosas. Ambas técnicas simplifican el proceso de aprendizaje al enfocarse en lo más relevante.

Funciones de Activación y Optimización

Las "Funciones de Activación" y la "Optimización" son conceptos clave en el campo del aprendizaje profundo y las redes neuronales artificiales. Ambos desempeñan un papel crucial en el proceso de entrenamiento de modelos de aprendizaje automático.

Las funciones de activación son como interruptores en las neuronas que deciden si deben activarse o no. La función ReLU es como un interruptor que se enciende cuando algo emocionante sucede. La optimización, por su parte, es como buscar el camino más eficiente para llegar a un destino, ajustando tu camino basado en las señales que encuentras en el camino.

Funciones de Activación: Encendiendo Neuronas

Las funciones de activación son bloques de construcción fundamentales en las redes neuronales artificiales. Se aplican a la salida de cada neurona en una capa de la red y determinan si una neurona debe "activarse" (enviar una señal) o no. Introducen no linealidad en el modelo, lo que permite a las redes neuronales aprender relaciones complejas en los datos.

Las funciones de activación son como chispazos que hacen que las neuronas se activen. Aquí hay algunas de las más usadas:

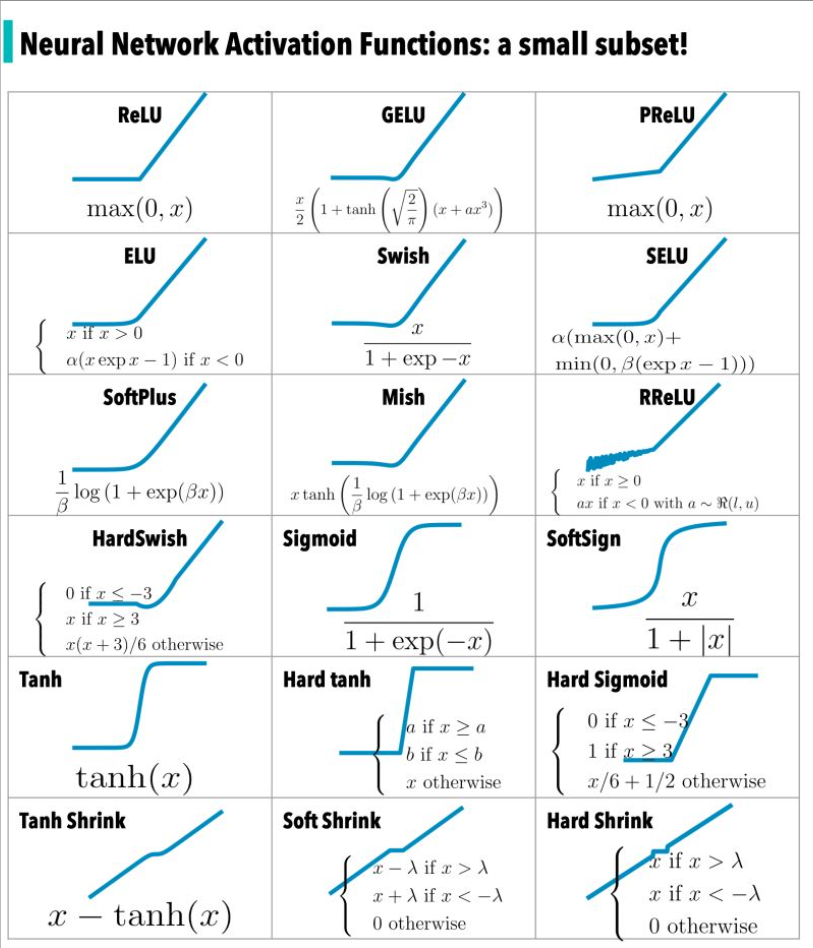
⭕ ReLU (Rectified Linear Unit): La función ReLU mapea los valores negativos a cero y mantiene los valores positivos sin cambios. Es simple y eficiente en términos de cálculos y ha demostrado ser efectiva en muchas aplicaciones.

Imagina que solo te emocionas si alguien te grita ¡Sí! ReLU se activa cuando una señal es positiva, y en caso contrario, permanece en silencio.

⭕ Sigmoid: Mapea los valores de entrada en un rango entre 0 y 1, lo que se asemeja a una curva en forma de "S". Aunque fue ampliamente utilizado en el pasado, se ha vuelto menos popular en redes neuronales profundas debido a problemas de desvanecimiento del gradiente.

Como una persona que toma decisiones basadas en su estado de ánimo. Sigmoid comprime los números entre 0 y 1, lo que lo hace útil para predecir probabilidades.

⭕ Tanh (Tangente Hiperbólica): Similar a la función sigmoide, pero mapea los valores de entrada en un rango entre -1 y 1. También puede sufrir de desvanecimiento del gradiente en redes profundas.

Imagina a alguien cambiando de humor de positivo a negativo y viceversa. Tanh tiene valores entre -1 y 1, lo que lo hace útil para centros de neurona.

⭕ Función Softmax: Utilizada comúnmente en la capa de salida de clasificación para convertir un conjunto de valores en una distribución de probabilidad. Es útil para problemas de clasificación multiclase.

Optimización:

La optimización se refiere al proceso de ajustar los parámetros (pesos y sesgos) de una red neuronal para minimizar una función de pérdida. La función de pérdida cuantifica la diferencia entre las predicciones del modelo y los valores reales del conjunto de datos. El objetivo es encontrar los valores de los parámetros que hagan que la función de pérdida sea lo más pequeña posible.

Existen varios algoritmos de optimización que se utilizan para actualizar los parámetros durante el entrenamiento de una red neuronal. Algunos de los algoritmos de optimización más populares son:

⭕ Descenso de Gradiente Estocástico (SGD): Actualiza los parámetros en función del gradiente de la función de pérdida calculada en un subconjunto aleatorio (lote) de datos en cada iteración.

Imagina que estás descendiendo una montaña nebulosa. En lugar de ver todo el paisaje a la vez, solo puedes ver una pequeña parte a través de la niebla. Para bajar más rápido, das pasos basados en la pendiente de la colina que ves en ese momento. A medida que avanzas, ajustas tus pasos para no dar saltos demasiado grandes ni pequeños. Eso es lo que hace el Descenso de Gradiente Estocástico: toma pequeños pasos en dirección descendente según la pendiente (gradiente) de la función de pérdida, pero solo mirando un pequeño grupo de datos a la vez.

⭕ Adam (Adaptive Moment Estimation): Un algoritmo de optimización adaptativo que ajusta las tasas de aprendizaje para cada parámetro según su historial de gradientes.

Imagina que estás explorando una colina con diferentes tipos de terreno. Al principio, das pasos grandes porque no estás seguro de qué tan empinada es la colina. Con el tiempo, ajustas el tamaño de tus pasos según cuánto hayas subido y bajado en diferentes partes de la colina. Adam hace algo similar: ajusta las tasas de aprendizaje para cada parámetro según cómo han cambiado los gradientes en el pasado, lo que ayuda a encontrar un camino más rápido hacia el fondo del valle.

⭕ RMSProp (Root Mean Square Propagation): Similar a Adam, RMSProp también ajusta las tasas de aprendizaje, pero de manera adaptativa en función de los gradientes pasados.

Supongamos que estás pescando en un río con corrientes cambiantes. A medida que avanzas, te das cuenta de que algunos lugares tienen corrientes más fuertes que otros. Ajustas tu enfoque en áreas donde las corrientes son más fuertes. RMSProp hace algo similar: adapta las tasas de aprendizaje según la rapidez con la que cambian los gradientes en diferentes partes del paisaje de la función de pérdida.

⭕ Momentum: Introduce un término de "momento" que ayuda a acelerar la convergencia y a superar mínimos locales.

Imagina que estás patinando sobre hielo. Cuando te encuentras en una colina, tu inercia te impulsa hacia arriba, incluso si la superficie es plana en ese momento. En términos de optimización, el "momentum" es como esa inercia. Ayuda a acelerar el movimiento en dirección a la dirección general del descenso, lo que puede ayudar a superar terrenos planos y llegar más rápido a un mínimo.

Estos algoritmos son como estrategias para bajar una montaña nebulosa (función de pérdida) de manera eficiente, ajustando los pasos y las velocidades en función de lo que se ha experimentado previamente. Cada uno tiene su propia forma de adaptarse al terreno y moverse hacia el mínimo global de la función de pérdida, que es donde queremos llegar para entrenar modelos de aprendizaje automático de manera efectiva.

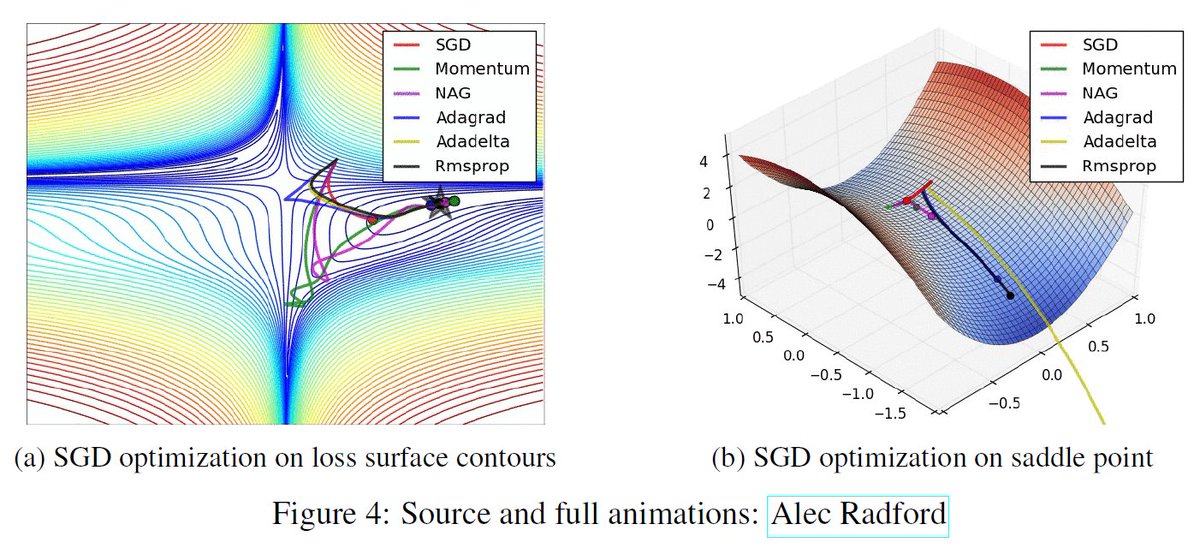
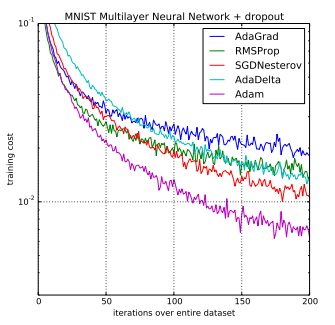
Estos son solo algunos ejemplos de funciones de activación y algoritmos de optimización en el contexto de las redes neuronales. La elección de la función de activación y el algoritmo de optimización adecuados puede tener un impacto significativo en el rendimiento y la eficiencia del modelo de aprendizaje profundo.

Kernel y Convolución: Procesando Información

El "Kernel" y la "Convolución" son conceptos fundamentales en el procesamiento de imágenes y en el campo del aprendizaje profundo, especialmente en las redes neuronales convolucionales (CNN, por sus siglas en inglés).

El kernel es como una lente que mira a través de los datos para encontrar patrones. La convolución es como mover la lente a lo largo de los datos para analizarlos en detalle.

⭕ Kernel: En el contexto del procesamiento de imágenes, un kernel es una matriz pequeña (generalmente de tamaño impar, como 3x3, 5x5, etc.) que se desliza sobre una imagen para realizar diversas operaciones, como detección de bordes, suavizado o realce de características. Cada elemento del kernel tiene un peso asociado y representa cómo contribuye a la transformación de la imagen. Los kernels se utilizan para aplicar operaciones de convolución a una imagen y extraer características relevantes.
⭕ Convolución: La convolución es una operación matemática que se utiliza para combinar dos funciones y producir una tercera. En el contexto del procesamiento de imágenes, la convolución se utiliza para resaltar características en una imagen o para aplicar efectos como el desenfoque. En términos simples, la convolución implica superponer un kernel sobre una región de la imagen y calcular la suma ponderada de los valores de píxeles correspondientes en la imagen y el kernel. Esta suma ponderada se coloca en un nuevo píxel en la imagen resultante. La operación de convolución se repite en toda la imagen para obtener una nueva imagen transformada.

En las redes neuronales convolucionales (CNN), la convolución se utiliza para extraer características relevantes de las imágenes. Los filtros (kernels) se aplican a la imagen de entrada mediante operaciones de convolución en diferentes capas. A medida que los filtros se desplazan sobre la imagen, detectan patrones y características específicas, como bordes, texturas y formas. Estas características se convierten en mapas de características que luego se utilizan para la clasificación, detección de objetos u otras tareas.

La convolución y el uso de kernels en CNN permiten a las redes neuronales aprender representaciones jerárquicas de características en las imágenes, lo que ha demostrado ser altamente efectivo para una variedad de tareas de visión por computadora, como el reconocimiento de objetos, segmentación de imágenes y más.

Ejemplo: Si estás buscando características en una imagen, como bordes, el kernel sería como una pequeña ventana que se desliza por la imagen, resaltando las áreas donde los bordes son más pronunciados.

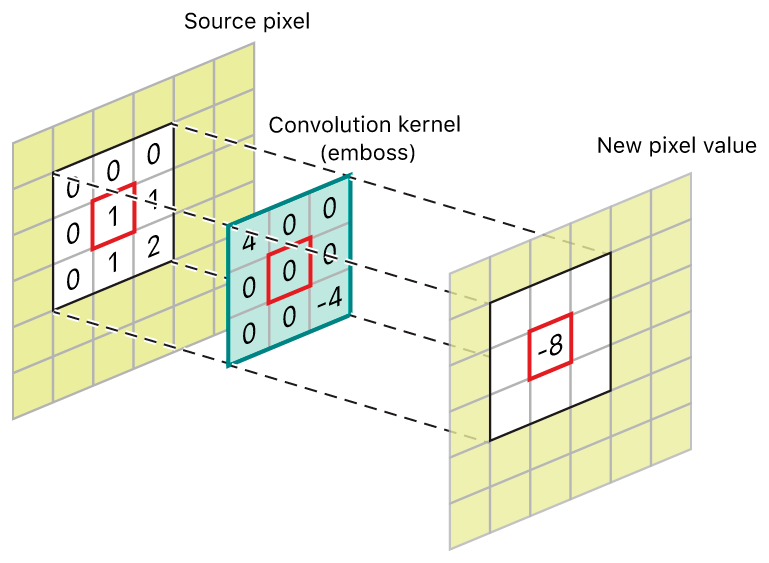
Estos conceptos, aunque suenan complejos, son los bloques de construcción que permiten a las máquinas aprender, razonar y tomar decisiones. Piensa en ellos como piezas de un rompecabezas gigante que, cuando se ensamblan, crean una imagen clara de cómo las máquinas pueden comprender y procesar información de manera sorprendentemente similar a nosotros.