Keras

En el vasto mundo del aprendizaje profundo, TensorFlow y Keras emergen como dos de las herramientas más poderosas y populares. Pero, ¿qué son exactamente y cómo se relacionan entre sí?

Tensorflow

Desarrollado por el equipo de Google Brain, TensorFlow es una biblioteca de código abierto que facilita la creación y entrenamiento de modelos de aprendizaje profundo. Su estructura de gráficos computacionales permite la representación de modelos complejos y su ejecución eficiente en diversas plataformas, desde CPUs hasta GPUs y TPUs. TensorFlow fue lanzado por primera vez el 9 de noviembre de 2015.

Por otro lado, Keras se presenta como una interfaz de alto nivel para construir y entrenar modelos de aprendizaje profundo. Originalmente desarrollado por François Chollet, Keras se integró con TensorFlow en 2017 como parte de la biblioteca de alto nivel de TensorFlow 2.0. Keras prioriza la facilidad de uso, la modularidad y la extensibilidad, lo que lo convierte en una opción popular para los desarrolladores de todos los niveles de experiencia.

Ahora que hemos establecido el contexto, exploremos algunas de las principales áreas de enfoque al trabajar con Keras en el contexto de TensorFlow.

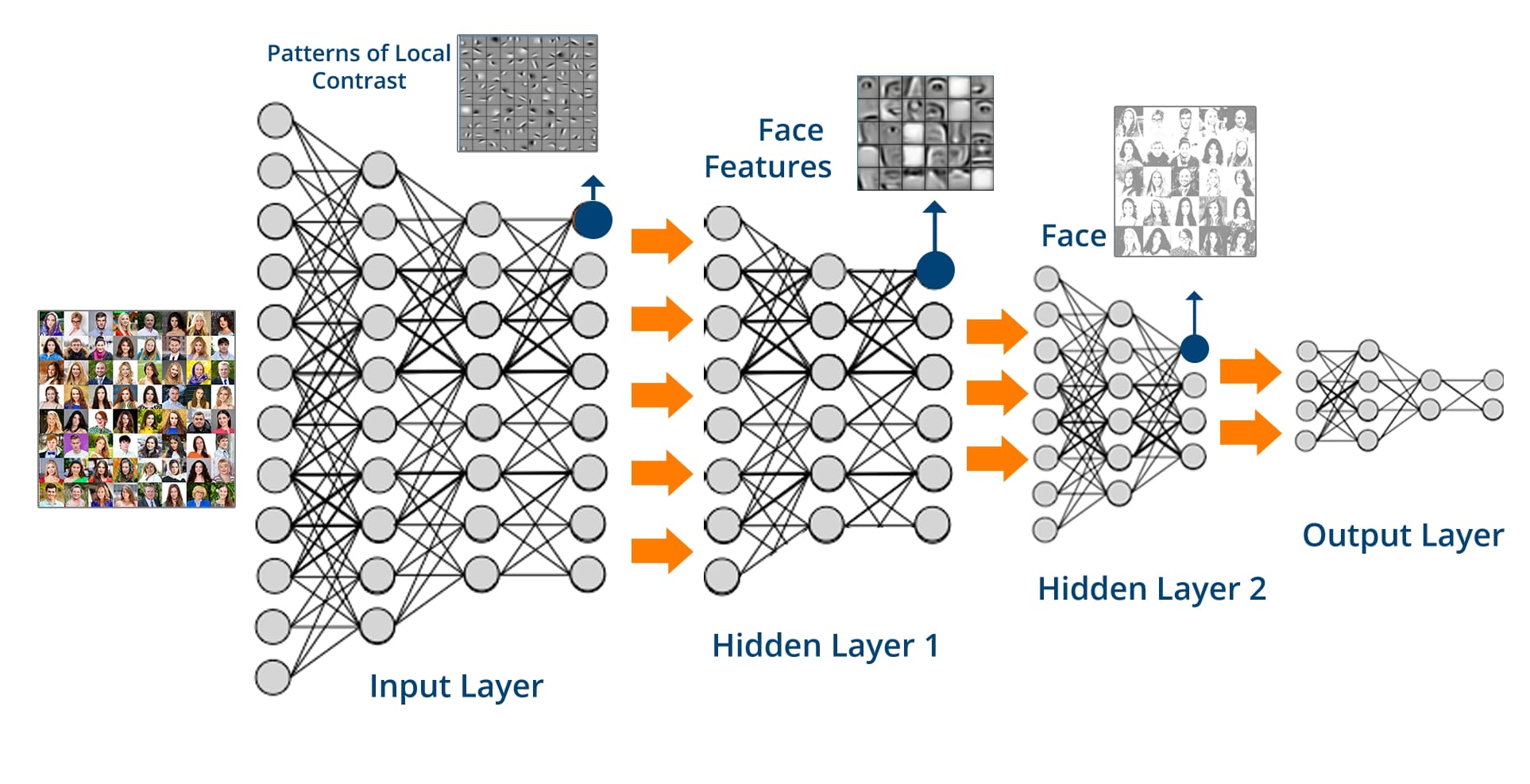
Creación de Redes Neuronales

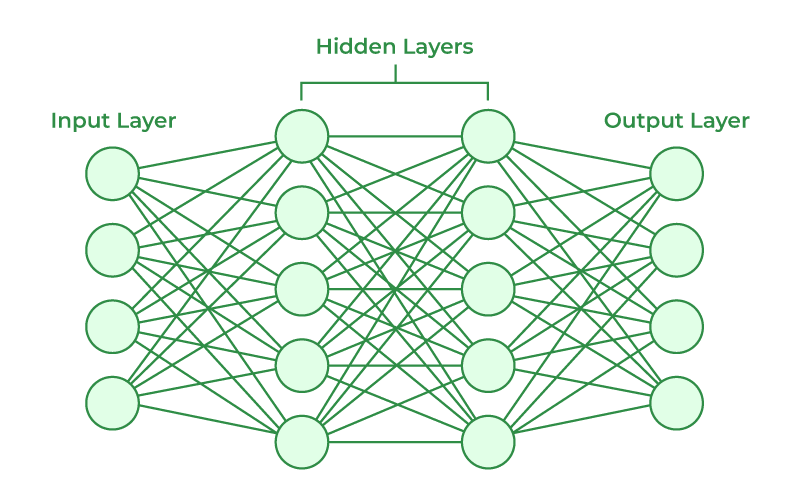
Keras ofrece una variedad de capas para construir redes neuronales, desde capas densas hasta convolucionales y recurrentes. Las redes neuronales convolucionales (CNN) son ideales para tareas de visión por computadora, mientras que las redes neuronales recurrentes (RNN) son eficaces para datos secuenciales como texto y series temporales.

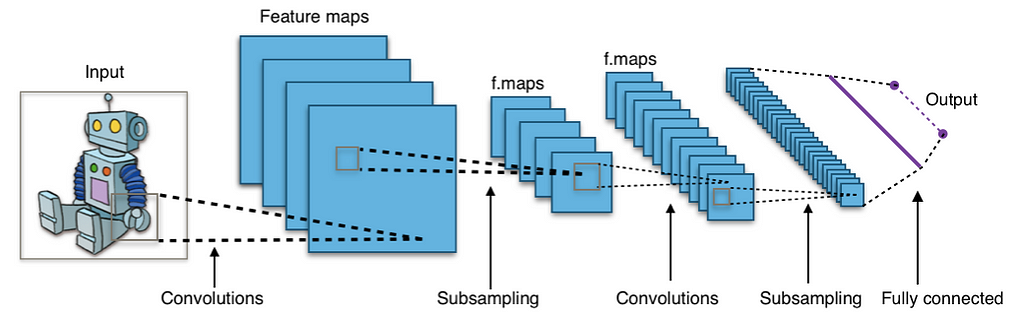
CNN

Las Redes Neuronales Convolucionales (CNN) son un tipo especializado de redes neuronales diseñadas principalmente para procesar datos de tipo grid, como imágenes. Funcionan mediante la aplicación de filtros convolucionales a la entrada, seguido de operaciones de agrupación (pooling) para reducir la dimensionalidad y finalmente, capas completamente conectadas para realizar la clasificación o regresión.

✦ Convolución: La convolución implica deslizar un filtro sobre la entrada y calcular la suma ponderada de los valores en la región de entrada correspondiente al filtro. Esto ayuda a detectar patrones locales como bordes, texturas o formas.
✦ Funciones de Activación: Después de cada operación de convolución, se aplica una función de activación (generalmente ReLU) para introducir no linealidad en la red.
✦ Agrupación (Pooling): Las capas de agrupación se utilizan para reducir la dimensionalidad de las características extraídas, manteniendo las características más importantes. La operación comúnmente usada es el max-pooling, que conserva el valor máximo en cada región de agrupación.
✦ Capas Completamente Conectadas: Después de varias capas de convolución y agrupación, las características se aplanan y se pasan a través de capas completamente conectadas para realizar la clasificación final.

Las CNN tienen la capacidad de aprender automáticamente características jerárquicas en los datos, lo que las hace extremadamente poderosas en tareas de visión por computadora como reconocimiento de imágenes, segmentación semántica y detección de objetos. Además, su capacidad de compartir pesos y su invarianza a la traslación las hacen eficientes en el manejo de datos de entrada con variaciones espaciales.

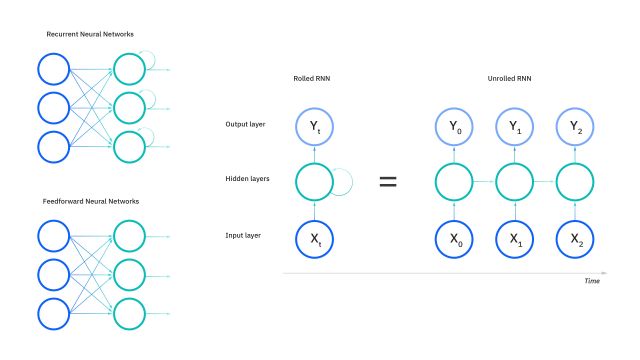
RNN

Las Redes Neuronales Recurrentes (RNN) son un tipo de red neuronal diseñada para trabajar con datos secuenciales, como series temporales, texto o audio. A diferencia de las redes feedforward tradicionales, las RNN tienen conexiones recurrentes que les permiten mantener y utilizar información sobre estados anteriores en la secuencia de entrada.

El funcionamiento básico de una RNN implica que cada neurona en la red tiene una "memoria" interna que recuerda la información procesada anteriormente. Esto le permite a la red capturar dependencias a lo largo del tiempo en los datos de entrada.

✦ Recurrencia: En cada paso de tiempo, la RNN toma una entrada y una representación de su estado anterior, y produce una salida y una actualización de su estado interno.
✦ Compartir Pesos: A diferencia de las redes feedforward, donde cada capa tiene sus propios pesos, las RNN comparten los mismos pesos a lo largo de todas las etapas de tiempo. Esto permite que la red aprenda patrones en secuencias de longitud variable.
✦ Backpropagation Through Time (BPTT): Durante el entrenamiento, se utiliza el algoritmo de retropropagación a lo largo del tiempo (BPTT) para calcular los gradientes y ajustar los pesos de la red.
✦ Problema de Desvanecimiento/Explotación del Gradiente: Las RNN tradicionales pueden sufrir de problemas de desvanecimiento o explosión del gradiente, lo que dificulta el entrenamiento de dependencias a largo plazo. Para abordar este problema, se han desarrollado variantes de RNN como Long Short-Term Memory (LSTM) y Gated Recurrent Unit (GRU), que incorporan mecanismos de memoria más sofisticados.

Las RNN son ampliamente utilizadas en aplicaciones que involucran datos secuenciales, como el procesamiento de lenguaje natural (NLP), la generación de texto, la traducción automática, la predicción de series temporales y más. Su capacidad para modelar dependencias a largo plazo las hace especialmente útiles en tareas donde la comprensión del contexto es crucial.

Hyperparametros

Los hiperparámetros son configuraciones que no se aprenden directamente del conjunto de datos durante el entrenamiento de un modelo de aprendizaje automático, sino que se establecen antes del proceso de entrenamiento. Estas configuraciones afectan el comportamiento y el rendimiento del modelo, pero deben ser ajustadas manualmente por el científico de datos o el ingeniero de aprendizaje automático.

En contraste, los parámetros del modelo, como los pesos en una red neuronal, son valores que se aprenden durante el entrenamiento a partir de los datos de entrenamiento.

Los hiperparámetros pueden incluir cosas como la tasa de aprendizaje, el tamaño del lote, el número de épocas, la arquitectura del modelo (número de capas y neuronas), las funciones de activación, los métodos de regularización, los optimizadores, entre otros.

Tasa de Aprendizaje (Learning Rate):

λ Descripción: Controla el tamaño de los pasos que el algoritmo de optimización toma durante el entrenamiento.
λ Casos de uso: Ajustar la tasa de aprendizaje es crucial para garantizar una convergencia estable del modelo. Se ajusta para mejorar la velocidad de convergencia y evitar oscilaciones.

Tamaño del Lote (Batch Size):

λ Descripción: Determina el número de ejemplos de entrenamiento que se utilizan en cada iteración de entrenamiento.
λ Casos de uso: Se ajusta para equilibrar la eficiencia computacional con la estabilidad del entrenamiento. Tamaños de lote más grandes pueden acelerar el entrenamiento, pero pueden aumentar la variabilidad del gradiente.

Número de Épocas (Number of Epochs):

λ Descripción: Define la cantidad de veces que el modelo verá todo el conjunto de datos durante el entrenamiento.
λ Casos de uso: Se ajusta para controlar la duración total del entrenamiento y evitar el sobreajuste. Se detiene el entrenamiento después de un número óptimo de épocas para evitar el sobreajuste.

Regularización (Regularization):

λ Descripción: Controla la complejidad del modelo al penalizar los pesos grandes.
λ Casos de uso: Se ajusta para evitar el sobreajuste al introducir una penalización en los pesos grandes. La regularización L1 y L2 son dos técnicas comunes utilizadas para este propósito.

Número de Capas y Neuronas (Number of Layers and Neurons):

λ Descripción: Define la arquitectura del modelo especificando el número de capas ocultas y el número de neuronas en cada capa.
λ Casos de uso: Se ajusta para controlar la capacidad del modelo y encontrar un equilibrio entre la capacidad de representación y el riesgo de sobreajuste.

Función de Activación (Activation Function):

λ Descripción: Determina cómo se combinan y transforman las entradas en una capa para producir la salida.
λ Casos de uso: Se ajusta para introducir no linealidad en la red y mejorar su capacidad de representación. ReLU, tanh y sigmoid son algunas de las funciones de activación comunes.

Inicialización de Pesos (Weight Initialization):

λ Descripción: Define cómo se inicializan los pesos del modelo antes del entrenamiento.
λ Casos de uso: Se ajusta para ayudar al modelo a converger más rápido y evitar problemas como el estancamiento del gradiente. Xavier y He son dos métodos de inicialización comunes.

Optimizador (Optimizer):

λ Descripción: Controla cómo se actualizan los pesos del modelo durante el entrenamiento.
λ Casos de uso: Se ajusta para mejorar la velocidad de convergencia y la estabilidad del entrenamiento. Adam, RMSprop y SGD son optimizadores comunes.

Función de Pérdida (Loss Function):

λ Descripción: Define cómo se calcula la discrepancia entre las predicciones del modelo y los valores reales.
λ Casos de uso: Se ajusta para adaptarse al tipo de problema que se está abordando. Entropía cruzada categórica, error cuadrático medio y pérdida de Huber son ejemplos comunes.

Aumento de Datos (Data Augmentation):

λ Descripción: Genera nuevas muestras de datos modificando las muestras existentes, como rotaciones, traslaciones y zooms.
λ Casos de uso: Se ajusta para mejorar la capacidad de generalización del modelo y evitar el sobreajuste. Es particularmente útil en problemas de visión por computadora donde se dispone de un conjunto de datos limitado.

Técnicas

Ajustar estos hiperparámetros de manera adecuada es crucial para obtener un rendimiento óptimo del modelo en una variedad de problemas de aprendizaje automático y profundamente aprendidos.

Estas son tres técnicas comunes utilizadas para ajustar los hiperparámetros de un modelo de aprendizaje automático:

Búsqueda en Cuadrícula (Grid Search):

λ Descripción: En la búsqueda en cuadrícula, se especifica una lista de valores posibles para cada hiperparámetro que se desea ajustar. Luego, se evalúa el rendimiento del modelo para todas las combinaciones posibles de valores de hiperparámetros utilizando una estrategia de validación cruzada.
λ Aplicación: Es útil cuando se tiene un conjunto de hiperparámetros relativamente pequeño y el espacio de búsqueda es manejable. Sin embargo, puede volverse computacionalmente costoso a medida que el número de hiperparámetros y valores posibles aumenta.

Búsqueda Aleatoria (Random Search):

λ Descripción: En la búsqueda aleatoria, se seleccionan aleatoriamente combinaciones de valores de hiperparámetros para evaluar el rendimiento del modelo. A diferencia de la búsqueda en cuadrícula, no se exploran todas las combinaciones posibles, lo que puede llevar a un ahorro de tiempo significativo.
λ Aplicación: Es útil cuando el espacio de búsqueda de hiperparámetros es grande y explorar todas las combinaciones posibles es computacionalmente costoso. A menudo, la búsqueda aleatoria puede encontrar combinaciones de hiperparámetros que son igual de buenas o mejores que las encontradas por la búsqueda en cuadrícula.

Optimización Bayesiana:

λ Descripción: La optimización bayesiana utiliza métodos basados en probabilidades para encontrar la combinación óptima de hiperparámetros. En lugar de evaluar todas las combinaciones posibles, utiliza información sobre iteraciones anteriores para decidir qué combinación de hiperparámetros explorar a continuación.
λ Aplicación: Es útil cuando el espacio de búsqueda es grande y costoso de explorar, ya que tiende a encontrar combinaciones de hiperparámetros que son óptimas en menos iteraciones en comparación con la búsqueda aleatoria o en cuadrícula. Es particularmente efectiva cuando el rendimiento del modelo es difícil de predecir y cuando el tiempo de cómputo es limitado.

Cada una de estas técnicas tiene sus propias ventajas y desventajas, y la elección de la técnica adecuada depende del problema específico que se esté abordando, así como de las restricciones computacionales y de tiempo disponibles.

Preprocesamiento de Datos y Aumento de Datos

El preprocesamiento de datos es una etapa crítica en el desarrollo de modelos de aprendizaje profundo. Keras proporciona herramientas para normalizar datos, manejar valores atípicos y convertir datos en formatos adecuados para la entrada del modelo. Además, el aumento de datos, como la rotación, el volteo y el recorte, puede ayudar a mejorar la generalización del modelo y prevenir el sobreajuste.

Aquí tienes algunos ejemplos de técnicas de normalización y preprocesamiento de datos:

Normalización de características:

θ Descripción: Ajusta los valores de las características para que tengan una media cercana a cero y una desviación estándar de uno.
θ Capa de aplicación: Puede aplicarse como una capa de preprocesamiento antes de la primera capa densa de la red neuronal.

Normalización por lotes (Batch Normalization):

θ Descripción: Normaliza las activaciones de cada capa utilizando la media y la desviación estándar de los datos en mini lotes durante el entrenamiento. Esto significa que los datos se normalizan con respecto a las estadísticas del lote en lugar de a cada instancia de forma individual.
θ Capa de aplicación: Se aplica típicamente después de las operaciones lineales (como las capas densas o convolucionales) y antes de las funciones de activación en cada capa.

Normalización por instancia (Instance Normalization)

θ Descripción: Normaliza las activaciones de cada instancia de manera independiente, lo que significa que las estadísticas de normalización se calculan para cada ejemplo en el conjunto de datos, en lugar de para lotes de ejemplos. No utiliza estadísticas agregadas de lotes.
θ Capa de aplicación: Se puede aplicar después de las operaciones lineales y antes de las funciones de activación en cada capa, similar a Batch Normalization.

La diferencia clave es que Batch Normalization normaliza las activaciones basándose en estadísticas agregadas de lotes de datos, mientras que Instance Normalization normaliza las activaciones de manera independiente para cada instancia de datos. Esto hace que Instance Normalization sea más adecuada para aplicaciones donde la estructura estadística de los datos varía significativamente entre instancias individuales, como el procesamiento de imágenes donde cada imagen puede tener diferentes iluminaciones, ángulos y estilos. Por otro lado, Batch Normalization suele ser más útil en redes neuronales profundas donde se pueden beneficiar de la estabilidad del entrenamiento que proporciona la normalización por lotes.

Escalamiento de características:

θ Descripción: Escala los valores de las características para que estén en un rango específico, como entre 0 y 1.
θ Capa de aplicación: Puede aplicarse como una capa de preprocesamiento antes de la primera capa densa de la red neuronal.

Escalamiento de características en la capa de salida:

θ Descripción: Escala los valores de salida de la red para que estén en un rango específico, como entre 0 y 1.
θ Capa de aplicación: Se realiza como parte de la capa de salida, especialmente en problemas de regresión donde se requieren valores específicos.

Escalamiento de píxeles (Pixel Scaling):

θ Descripción: Escala los valores de los píxeles de una imagen a un rango específico, como entre 0 y 1.
θ Capa de aplicación: Puede aplicarse como una capa de preprocesamiento antes de la primera capa de una red neuronal convolucional (CNN).

Aumento de datos mediante espejo y rotación:

θ Descripción: Esta técnica implica la aplicación de transformaciones como el volteo horizontal, el volteo vertical y la rotación a las imágenes de entrada. Por ejemplo, una imagen original puede ser espejada horizontalmente, verticalmente o rotada en diferentes ángulos para generar nuevas muestras de entrenamiento. El objetivo es introducir variabilidad en los datos de entrenamiento sin cambiar la etiqueta asociada. Esto ayuda al modelo a generalizar mejor y a ser más robusto ante diferentes orientaciones y posiciones de objetos en las imágenes.
θ Capa de aplicación: Se aplica a conjuntos de datos de imágenes durante la fase de preprocesamiento, antes o durante el entrenamiento del modelo. Puede ser implementado utilizando bibliotecas de procesamiento de imágenes como OpenCV, PIL (Python Imaging Library) o mediante funciones integradas en bibliotecas de aprendizaje profundo como TensorFlow o PyTorch.

Aumento de datos mediante cambio de brillo y contraste:

θ Descripción: Esta técnica implica la aplicación de cambios en el brillo, contraste y/o saturación de las imágenes de entrada. Estos cambios pueden simular diferentes condiciones de iluminación y mejorar la capacidad del modelo para generalizar a imágenes con diferentes niveles de luz y contraste. Por ejemplo, se pueden aplicar aumentos de brillo y contraste multiplicando cada píxel por un factor de escala adecuado.
θ Capa de aplicación: Similar al aumento de datos mediante espejo y rotación, se aplica a conjuntos de datos de imágenes durante la fase de preprocesamiento o durante el entrenamiento del modelo. También puede ser implementado utilizando bibliotecas de procesamiento de imágenes o funciones integradas en bibliotecas de aprendizaje profundo.

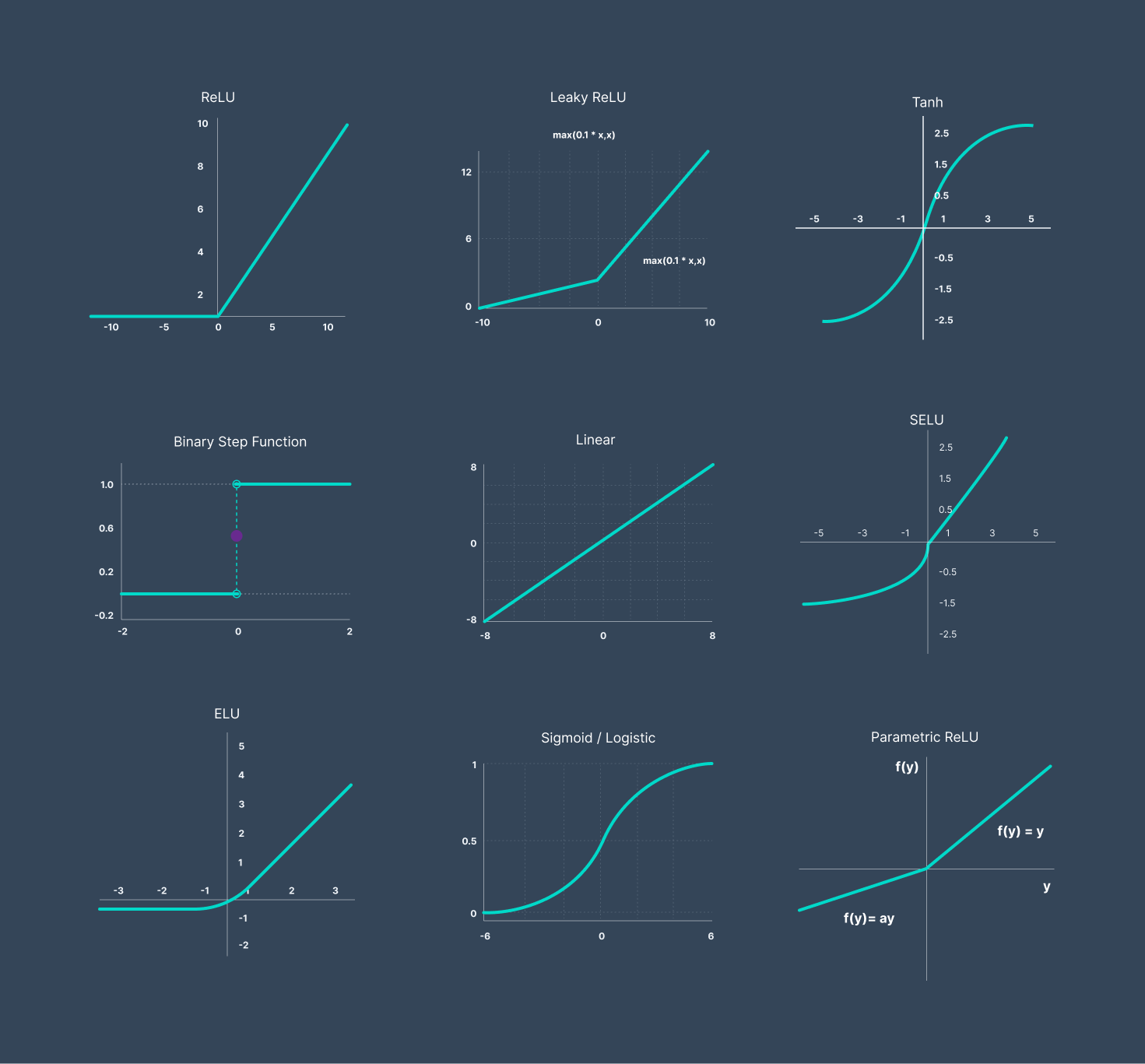
Funciones de Activación

Las funciones de activación son componentes esenciales en cada neurona, ya que introducen no linealidad en la red. Algunas de las funciones de activación comunes incluyen ReLU (Rectified Linear Unit), sigmoides y tangentes hiperbólicas. La elección de la función de activación puede afectar significativamente el rendimiento y la capacidad de aprendizaje del modelo.

Aquí hay una descripción de las funciones de activación más comunes:

ReLU (Rectified Linear Unit):

δ Función: \( f(x) = \max(0, x) \)
δ Ventajas: Simple, eficiente computacionalmente y ayuda a evitar el problema del desvanecimiento del gradiente.
δ Modelos: CNNs y DNNs para una variedad de tareas.

Leaky ReLU:

δ Función: \( f(x) = \max(\alpha x, x) \), donde \( \alpha \) es un valor pequeño.
δ Ventajas: Ayuda a mitigar el problema de "neuronas muertas" que pueden ocurrir con ReLU.
δ Modelos: CNNs y DNNs donde se quiere evitar la inactivación completa de neuronas.

ELU (Exponential Linear Unit):

δ Función: \( f(x) = \begin{cases} x, & \text{si } x > 0 \\ \alpha (e^x - 1), & \text{si } x \leq 0 \end{cases} \), donde \( \alpha \) es un valor pequeño.
δ Ventajas: Puede ayudar a reducir el problema del desvanecimiento del gradiente y proporciona una activación suave para valores negativos.
δ Modelos: CNNs y DNNs donde se busca una alternativa suave a ReLU.

Sigmoid:

δ Función: \( f(x) = \frac{1}{1 + e^{-x}} \)
δ Ventajas: Útil para producir salidas entre 0 y 1, útil en modelos donde se requiere una probabilidad como salida.
δ Modelos: Modelos de clasificación binaria y en capas de salida de redes generativas.

Tanh (Tangente Hiperbólica):

δ Función: \( f(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} \)
δ Ventajas: Produce salidas entre -1 y 1, lo que puede ayudar a mitigar el problema de la "desaparición" de gradientes.
δ Modelos: RNNs, especialmente en capas ocultas donde se necesita una salida que oscile entre -1 y 1.

Softmax:

δ Función: \( f(x_i) = \frac{e^{x_i}}{\sum_{j} e^{x_j}} \) para cada elemento \( x_i \).
δ Ventajas: Se utiliza para producir una distribución de probabilidad sobre múltiples clases.
δ Modelos: Capa de salida de modelos de clasificación multiclase.

Linear (Identidad):

δ Función: \( f(x) = x \)
δ Ventajas: Conserva la información original sin introducir no linealidad.
δ Modelos: En raras ocasiones, como en modelos donde se desea una salida lineal.

Hard Tanh:

δ Función: Similar a tanh pero con valores truncados a -1 y 1.
δ Ventajas: Similar a tanh pero más rápido de calcular.
δ Modelos: Modelos donde se prefiere tanh pero con menor costo computacional.

GELU (Gaussian Error Linear Unit):

δ Función: \( f(x) = x \cdot \Phi(x) \), donde \( \Phi(x) \) es la función de distribución acumulativa normal estándar.
δ Ventajas: Introduce una no linealidad suave que puede mejorar el rendimiento en algunas aplicaciones.
δ Modelos: CNNs y DNNs, especialmente en modelos de transformers.

Swish

δ Función: \( f(x) = x \cdot \text{sigmoid}(x) \)
δ Ventajas: Se ha demostrado ser una alternativa efectiva en algunos casos.
δ Modelos: CNNs y DNNs, especialmente en modelos donde ReLU no funciona bien.

Mish

δ Función: \( f(x) = x \cdot \tanh(\text{softplus}(x)) \)
δ Ventajas: Se ha demostrado experimentalmente que funciona bien en algunos casos.
δ Modelos: CNNs y DNNs, especialmente en modelos donde ReLU no funciona bien.

Mish proporciona una activación suave y no lineal que puede ayudar a mitigar algunos problemas de activación, similar a Swish. Su capacidad para adaptarse a diferentes tipos de datos y arquitecturas la convierte en una opción valiosa en el arsenal de funciones de activación para diseñadores de modelos de aprendizaje profundo. Sin embargo, en términos de rendimiento, Mish no ha demostrado consistentemente superar a funciones de activación más establecidas como ReLU o incluso Swish.

La elección de la función de activación depende en gran medida del problema que se esté abordando, la arquitectura del modelo y la experiencia empírica con los datos y técnicas de entrenamiento. Experimentar con varias funciones de activación puede ser beneficioso para determinar cuál funciona mejor para una tarea específica.

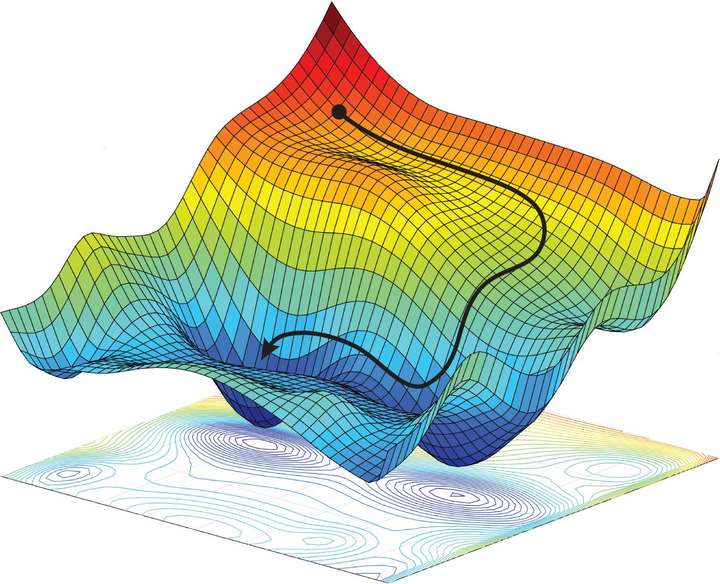
Algoritmos de Optimización

La optimización es crucial para entrenar modelos de manera efectiva. Keras ofrece una variedad de funciones de pérdida y optimizadores para adaptarse a diferentes tipos de problemas y datos. Algunos optimizadores populares incluyen SGD (Descenso de Gradiente Estocástico), Adam y RMSprop.

Aquí hay una descripción de las funciones de optimización más comunes:

SGD (Stochastic Gradient Descent):

δ Tasa de aprendizaje óptima: Entre 0.01 y 0.1.
δ Descripción: Actualiza los parámetros en la dirección opuesta al gradiente de la función de pérdida.
δ Aplicaciones: Problemas de clasificación y regresión en conjuntos de datos grandes.

Adam (Adaptive Moment Estimation):

δ Tasa de aprendizaje óptima: Entre 0.001 y 0.01.
δ Descripción: Combina los conceptos de momentum y RMSprop, adaptando la tasa de aprendizaje para cada parámetro.
δ Aplicaciones: Ampliamente utilizado en una variedad de problemas de aprendizaje profundo, especialmente en redes neuronales convolucionales (CNNs) y recurrentes (RNNs).

RMSprop (Root Mean Square Propagation):

δ Tasa de aprendizaje óptima: Entre 0.001 y 0.01.
δ Descripción: Divide la tasa de aprendizaje por una estimación del tamaño de los gradientes acumulados en el pasado reciente.
δ Aplicaciones: Recomendado para problemas donde los gradientes pueden variar significativamente.

Adagrad (Adaptive Gradient Algorithm):

δ Tasa de aprendizaje óptima: Entre 0.01 y 0.1.
δ Descripción: Ajusta la tasa de aprendizaje de cada parámetro en función de la frecuencia de actualización de ese parámetro.
δ Aplicaciones: Útil en problemas de optimización convexa con características dispersas.

Adadelta:

δ Tasa de aprendizaje óptima: No se requiere especificar explícitamente una tasa de aprendizaje.
δ Descripción: Similar a RMSprop pero normaliza la tasa de aprendizaje mediante una estimación del tamaño de los cambios de parámetros.
δ Aplicaciones: Buen rendimiento en problemas con gradientes cambiantes y datos ruidosos.

AdaMax:

δ Tasa de aprendizaje óptima: Entre 0.001 y 0.01.
δ Descripción: Variante de Adam que utiliza la norma infinito para normalizar el tamaño del gradiente.
δ Aplicaciones: Similar a Adam pero con menos sensibilidad a los cambios en la tasa de aprendizaje.

Nadam (Nesterov-accelerated Adaptive Moment Estimation):

δ Tasa de aprendizaje óptima: Entre 0.001 y 0.01.
δ Descripción: Combina las ventajas de Nesterov Accelerated Gradient (NAG) con Adam.
δ Aplicaciones: Adecuado para una variedad de problemas de aprendizaje profundo.

FTRL (Follow-The-Regularized-Leader):

δ Tasa de aprendizaje óptima: Entre 0.1 y 1.0.
δ Descripción: Utiliza un algoritmo de minimización de pérdida regularizado que se adapta a la tasa de aprendizaje en función de la frecuencia de actualización de cada característica.
δ Aplicaciones: Útil en problemas de regresión logística con características dispersas.

AMSGrad:

δ Tasa de aprendizaje óptima: Entre 0.001 y 0.01.
δ Descripción: Variante de Adam que evita la degradación del desempeño asociada con el algoritmo original Adam.
δ Aplicaciones: Aborda un problema de convergencia no deseado en Adam, donde la tasa de aprendizaje puede disminuir rápidamente para algunas características.

Es importante tener en cuenta que los valores de la tasa de aprendizaje pueden variar dependiendo del conjunto de datos, la arquitectura del modelo y la tarea específica que se esté abordando. Experimentar con diferentes valores de tasa de aprendizaje y optimizadores es crucial para obtener los mejores resultados en un problema dado.

Técnicas para Mejorar el modelo

Además de las técnicas mencionadas anteriormente, Keras ofrece herramientas adicionales para mejorar la capacidad predictiva de los modelos. El early stopping, por ejemplo, detiene el entrenamiento del modelo cuando la pérdida en el conjunto de validación deja de disminuir, lo que ayuda a evitar el sobreajuste. La normalización de datos también es crucial para asegurar que todas las características contribuyan de manera equitativa al proceso de entrenamiento.

Algunas técnicas adicionales que pueden mejorar el rendimiento de un modelo de aprendizaje profundo son:

Early Stopping:

Σ Descripción: Detiene el entrenamiento del modelo cuando la métrica de rendimiento en un conjunto de validación deja de mejorar, con el fin de evitar el sobreajuste.
Σ Aplicación: Se utiliza durante el entrenamiento del modelo para evitar el sobreajuste y mejorar la generalización.

Dropout:

Σ Descripción: Aleatoriamente apaga una fracción de las neuronas durante el entrenamiento para evitar la coadaptación de las neuronas.
Σ Aplicación: Se aplica en las capas ocultas de la red para mejorar la capacidad de generalización y evitar el sobreajuste.

Regularización L1 y L2:

Σ Descripción: Penaliza los pesos de la red neuronal para evitar que se vuelvan demasiado grandes.
Σ Aplicación: Se aplica como una técnica de regularización en las capas densas para evitar el sobreajuste y mejorar la generalización.

Reducción de la tasa de aprendizaje (Learning Rate Decay):

Σ Descripción: Reduce gradualmente la tasa de aprendizaje durante el entrenamiento para ayudar al modelo a converger de manera más estable.
Σ Aplicación: Se aplica durante el entrenamiento para evitar oscilaciones y mejorar la convergencia del modelo.

Ensemble Learning:

Σ Descripción: Combina las predicciones de múltiples modelos para mejorar el rendimiento predictivo.
Σ Aplicación: Se utilizan múltiples modelos entrenados de forma independiente y luego se combinan sus predicciones, por ejemplo, mediante votación o promedio ponderado.

Ajuste de hiperparámetros (Hyperparameter Tuning):

Σ Descripción: Optimiza los hiperparámetros del modelo, como la tasa de aprendizaje, el tamaño del lote y la arquitectura de la red, para mejorar el rendimiento.
Σ Aplicación: Se utiliza mediante técnicas como la búsqueda en cuadrícula, la búsqueda aleatoria o la optimización bayesiana para encontrar la combinación óptima de hiperparámetros.

Estas técnicas complementarias pueden combinarse y ajustarse según las características específicas del problema y los datos para mejorar aún más el rendimiento del modelo de aprendizaje profundo.

Keras y TensorFlow ofrecen un ecosistema robusto y flexible para el desarrollo de modelos de aprendizaje profundo. Desde la construcción de redes neuronales hasta la optimización y el preprocesamiento de datos, estas herramientas proporcionan a los desarrolladores las herramientas necesarias para abordar una amplia gama de problemas en el campo del aprendizaje automático y la inteligencia artificial.

Ejemplos

Haz click aquí para ver algunos ejemplos de uso con Keras.